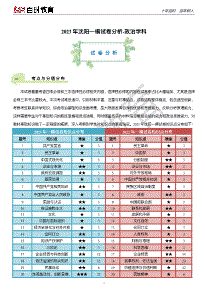
十年百时百年树人2023年沈阳市高中三年级教学质量检测(一)试卷分析一考点与分值分布本次一模考试的考点的覆盖面比较广,基本涉及到高中各章节的考查点,能够很好的考查考生对各个模块基础知识的掌握情况,同时对各个章节之间综合问题进行了细致的考查,方便各位考生对自己在一轮复习后各章节内容的检验以及确定二轮复习中各个模块的复习方向和侧重点的调整.具体知识点分布如下:2023年一模考试知识点分布题号知识点难度分值1集合★52复数★53平面向量★★54函数★★105充分必要条件的判断★56直线与圆★★57不等式★★★58三角函数★★59二项式定理★★510排列组合★★511立体几何★★1012解三角形★★1213数列★★151十年百时百年树人14概率分布★★★1715空间向量与立体几何★★★1216圆锥曲线★★★1717导数综合★★★12二命题趋势分析一模试卷从整体来看难度中等偏难,加入了复杂情景题型,考查了学生的数学思想方法,选择题采用8道单选+4道多选的题型模式,整体难度中上,涵盖了大部分的考点综合题型,其中第4题考查的新定义问题,要注意对定义的理解,都为常规题型的拓展题型,大部分类似题型在平时练习中都有出现,需要学生能够把思路方法进行迁移;多选整体的难度都不高;填空题整体难度相对偏难,其中第15题涉及到的立体几何问题,对学生在立体几何图形的理解上要求比较高;第16题有多种解题方法,涉及到各个知识点领域的综合应用,考查学生的综合理解分析能力,难度比较大;解答题整体契合我们平时练习的题型分布,难度中上,各个题虽然中规中矩但是在题型细节上会有些许的变化,很好的考查了学生的数学思想方法,其中第18题中的三选二也是出现次数不多的题型考查;第19题的建系位置也没有延续常规的考查;第20题的比赛规则与奖金的结合,多方位的考查学生在概率分布题型的思维;第21,22题涉及常规的圆锥和导数题型,难度较大,需要学生能够理解好图形以及函数形式的变化规律,考查学生的综合思维能力;整体题目难易程度中等偏上,主要考查学生各章节内容的综合应用,思路方法的迁移以及实际应用问题的处理,整体难中易程度比例为2:3:5.以下几个题目相对容易出现错误:2十年百时百年树人一、单项选择题第4题:考查的新定义问题,要注意对定义以及对立体几何图形的理解;第7题:考查导数的切线放缩以及飘带函数的直接应用;第8题:圆锥曲线的细节考查,利用条件确定四边形为菱形,进而通过Q点的坐标或者焦点三角形性质求取;二、多项选择题第10题:;利用算数平均值与几何平均值的关系和数列的综合进行判断,思路相对较难三、填空题第15题:立体几何问题,对学生在立体几何图形的理解上要求比较高;第16题:解题方法多样,需要注意各个方法应用的细节,考查学生对题型整体的分析与理解四、解答题第17题:向量坐标运算以及裂项相消方法都是常规的考查;第18题:解三角形的常规考查,涉及到三选二的题型不常见,需要学生对每个条件有整体的理解;第19题:第一问常规的立体几何证明题型;第二问利用空间向量求夹角,注意建系的位置证明,以及各个点的坐标,涉及的公式应用平时练习中经常出现,注意计算问题;第20题:新定义比赛规则和奖金分布综合问题,考查学生在规则上以及奖金比例的理解,多方位的考查需要学生对整体有个很好的理解,概率分布列的求取属于常规题型,计算不要马虎;第21题:圆锥曲线中双曲线综合问题,第一问直接利用题中条件得出结果;第二问利用直线与双曲线联立,利用参数表示面积,根据面积条件确定参数范围;第22题:导数涉及的单调性的分类,零点题型,属于常规题型,难度较大,需要学生能够理解函数形式以及图像的变化规律,考查学生的综合思维能力;。试题分析x1第1题:已知集合Axx2x60,集合Bx0,则A∩B=()x4A.x4x3B.x2x3C.x2x1D.x4x13十年百时百年树人解析:考查集合交集的运算,综合了一元二次不等式以及分式不等式的解法,利用数轴确定交集范围答案:C第2题:已知复数z满足(z+i)i=2+3i,则z=()A.2B.3C.13D.32解析:复数运算典型题型,注意复数的模的运算公式答案:D第3题:命题p:直线ykxb与抛物线x22py有且仅有一个公共点,命题q:直线ykxb抛物线x22py相切,则命题p是命题q的()A.充分不必要条件B.必要不充分条件C.充要条件D.非充分非必要条件解析:充分必要条件的判断,常规题型,注意命题的前后顺序答案:C第4题:刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2与多面体在该点的面角和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和,则正八面体(八个面均为正三角形)的总曲率为()A.2B.4C.6D.84十年百时百年树人解析:新定义题型,根据题中所给曲率的定义,结合立体几何的图形性质得出结论答案:B第5题:如图是函数H(x)图像的一部分,设函数f(x)cosx,g(x)|x|1,则H(x)可以表示为()A.f(x)g(x)B.f(x)g(x)C.f(x)g(x)f(x)D.g(x)解析:函数图像的判断,考查函数的各个性质,根据图像中的特殊点以及性质,逐个验证排除即可答案:D第6题:甲、乙、丙、丁、戊、己6人站成一排拍合照,要求甲必须站在中间两个位置之一,且乙、丙2人相邻,则不同的排队方法共有()A.24种B.48种C.72种D.96种解析:排列组合典型题型,分类与分步的综合考查答案:Clnt23第7题:已知a,b,cln,则a,b,c的大小关系为()t52A.abcB.acbC.bcaD.cab5十年百时百年树人解析:考查导数的切线放缩以及飘带函数的直接应用;答案:Ax2y2第8题:已知椭圆1(ab0)的右焦点为F,过F作倾斜角为120°的直线l交该椭圆a2b2上半部分于点P,以FP,FO(O为坐标原点)为邻边作平行四边形OFPQ,点Q恰好也在该椭圆上,则该椭圆的离心率为()132A.B.31C.D.222解析:圆锥曲线的细节考查,利用条件确定四边形为菱形,进而通过Q点的坐标或者焦点三角形性质求取答案:B第9题:某产品的质量指标值服从正态分布N100,2,则下列结论正确的是()A.越大,则产品的质量指标值落在(99.9,100.1)内的概率越大B.该产品的质量指标值大于100的概率为0.5C.该产品的质量指标值大于100.01的概率与小于99.99的概率相等D.该产品的质量指标值落在(99.9,100.2)内的概率与落在(100,100.3)内的概率相等解析:正态分布的直接考查,利用正态分布图像的对称性逐一验证各个选项即可答案:BC第10题:是各项均为正数的等差数列,其公差是等比数列,若,and0,bna1b1,a2022b20226十年百时百年树人则()A.a100b100B.a100b100C.a2023b2023D.a2023b2023解析:利用算数平均值与几何平均值的关系和数列的综合进行判断答案:AD第11题:已知圆C:(x1)2(y2)22,点M是直线l:yx1上的动点,过点M作圆C的两条切线,切点分别为A,B,则下列说法正确的是()A.切线长|MA|的最小值为6B.四边形ACBM面积的最小值为23C.若PQ是圆C的一条直径,则MPMQ的最小值为713D.直线AB恒过,22解析:直线与圆的综合应用,利用解析几何的各个公式来逐个验证各个选项即可答案:ABD第12题:声音是由物体振动产生的声波,纯音的数学模型是函数yAsint,我们听到的声音是由纯音合成的,称之为复合音,若一个复合音的数学模型是函数f(x)2sinxsin2x,则下列结论中正确的为()A.f(x)在,上是增函数44B.f(x)的最小正周期为7十年百时百年树人33C.f(x)的最大值为2272D.若fxfx,则xx12412min3解析:三角函数图像的考查,可以利用图像的叠加确定函数图像的基本性质,再逐一验证各个选项即可答案:ACD第13题:已知向量a(cos,2),b(sin,1),且ab,则tan等于________.4解析:向量坐标运算和三角函数恒等变换的综合应用,考查向量的运算公式和三角恒等变换公式答案:3第14题:若20232023,则被除的余数是(1x)a0a1xa2023xa0a2a4a20225________.解析:考查赋值法在二项式定理中的应用,综合二项式定理的性质确定余数答案:4第15题:三棱锥ABCD中,ABCCBDDBA60,BCBD2,点E为CD中点,△ABE的面积为22,则AB与平面BCD所成角的正弦值为________,此三棱锥外接球的体积为________.解析:立体几何综合题型,考查学生对图形的整体理解,利用几何法构造夹角或者三余弦定理解决,通过立体几何图形确定外接球半径8十年百时百年树人632答案:,33第16题:已知实数x,y满足x2y2xy1,则2x2y2的最大值为________.解析:利用三角换元或者判别式法求取,考查学生对这两个方法的应用的细节把握623答案:3第17题:设*,向量nNAB(n1,1),AC(n1,4n1),anABAC.()令,求证:数列为等差数列;1bnan1anbn1113(2)求证:.a1a2an4解析:向量坐标运算与数列相结合,利用向量坐标运算确定数列的通项,根据通项的形式,利用数列的裂项相消证明不等式设*,向量答案:nNAB(n1,1),AC(n1,4n1),anABAC.()令,求证:数列为等差数列;1bnan1anbn1113(2)求证:.a1a2an4()2,21ann2nan1n2n12n2,bn2n3bn12n1,所以数列为等差数列bnbn12bn.111111131113(2)1.a1a2an22n1n242n1n249十年百时百年树人第18题:在△ABC中,角A,B,C的对边分别为a,b,c.已知sinA3cosA0.(1)求角A的大小;(2)给出以下三个条件:①;②222;③a43,b4bac10b0S△ABC153.若这三个条件中仅有两个正确,请选出正确的条件并回答下面问题:(i)求sinB的值;(ii)BAC的角平分线交BC于点D,求AD长.解析:解三角形综合题型考查,利用条件确定内角大小,结合①②③的条件验证正误,利用正余弦定理以及角平分线的比例关系求解2答案:(1)tanA3,A.3222(2)选择②;③.bac10b0,可以得到c10,1S△153bcsinAb6ABC2ab14633sinBa14,由正弦定理sinAsinB3sinB14215SABCSABDSACDAD4第19题:如图,在矩形ABCD中,AB=4,E为边CD上的点,CB=CE,以BE为折痕把CBE折42起,使点C到达点P的位置,且使二面角PBEC为直二面角,三棱锥PABE的体积为.3(1)证明:平面PAB⊥平面PAE;(2)求二面角BPAD的余弦值。10十年百时百年树人解析:空间向量与立体几何的常规题型,建系或是证明上都是常见形式,利用条件确定各个棱的棱长,主要是注意建系的位置,各个点的坐标以及向量坐标的准确性以及计算不要马虎答案:(1)证明:有CBCE,设BE的中点
数学分析
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP