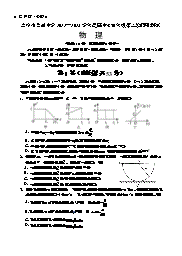吉林市普通中学2022—2023学年度高中毕业年级第二次调研考试对于C选项：令g(x)f(2x)f(2x)，x(0，2).数学试题参考答案4x2(x212)一、单项选择题：本大题共小题，每小题分，共分.g(x)f(2x)f(2x)0，8540(4x2)212345678g(x)在(0，2)上递减，即g(x)g(0)0.DCADDDBCx，gxfxfx，fxfx.二、多项选择题：本大题共4小题，共20分.全部选对的得5分，部分选对的得2分，有选错的得0022(22)(42)(2)0(42)(2)分.，f(x2)f(x3)f(4x2)f(x3).9101112又在（，）上单调递增，，即，选项正确；f(x)24x2x3x2x34CADBDACDABCx28x28对于D选项：f(x)f(x)，12，122x2x三、填空题：本大题共4个小题,每小题5分，共20分.12xx8即（）（12）1x1x20.13.,14.715.2697；a116.[0,2)2xx4121611题解析：，x1x2x1x2.x1x28x38解析：f(x)x22.xx（）2（）2（16）2（）x2x1x1x24x1x24x1x2x1x2令f(x)0，则x2；令f(x)0，则x2且x0；1616令txx，t0，则（xx）2（）24t（）22t2t332102432，f(x)的增区间为：（2，），减区间为：（，0），（0，2）.1221tt故D选项正确.对于A选项：f(2)6且g(x)有三个零点，a6，即A选项正确；1616[另解：由f(x)f(x)f(x)，可得xx0，故B错；xx，由基本x28x281612313xx23xx对于B选项：当x0时，f(x)f(x)()()0，13232x2xx不等式可得C对.]f(x)f(x).15题解析：，f(x1)f(x3)f(x1)f(x3)f(x3).（1）由斐波那契数Fn除以4的余数按原顺序构成的数列{an}，是以6为最小正周期的数列，fx在（，）上单调递减，xx，即xx，即B选项错误；所以()013130a1a2a3a2023833712697高三数学试题答案第1页（共8页）（2）由斐波那契数F的递推关系可知：n2时FFF，且FF1，Fa6040nn2nn1122024系，可得：13.215.214(cm)100100所以F1F2F2022(F3F2)(F4F3)(F2024F2023)F2024F2a1.所以，抽取的总样本的平均数为14cm.·······································································5分（也可直接由性质aaaaa1得出结论）123nn2（Ⅱ）男生样本的平均数为，样本方差为2；女生样本的平均数为，x13.2s113.36y15.215题说明：样本方差为2；由（Ⅰ）知，总样本的平均数为.s217.5614本题源自人教A版选择性必修第二册P10—P11页阅读与思考部分内容.记总样本的样本方差为2，斐波那契数列满足：，，*，s{an}a11a21anan-1an2(nN,n2)1则s222························9分该数列通项公式为：115n15n（用无理数表示有理数的典型代表）{60[13.36(13.214)]40[17.56(15.214)]}16an[()()]100522所以，估计高三年级全体学生的坐位体前屈成绩的方差为16.·········································10分n常考性质：（1）a2a2a2a2aa，即a2aa.123nnn1knn1（注：本次考试给出了分层随机抽样的方差公式，但是此公式需要记忆，请老师在教学中强调并指导k1学生完成公式的推导.）n（2），即.a1a3a5a2n-1a2na2k1a2nk118．【解析】n（Ⅰ）（法一）利用余弦定理（3），即.因为，由余弦定理，得a2a4a6a2na2n11a2ka2n11bcosCccosB6k1a2b2c2a2c2b2nbca6··································································4分（4），即.2ab2aca1a2a3anan21akan21k1（法二）利用正弦定理因为bcosCccosB6，由正弦定理，得（5）a4k为3的倍数.2R(sinBcosCsinCcosB)62Rsin(BC)6四、解答题2RsinA6即a6····························································································4分．【解析】17（Ⅱ）选择①：mn100abc6（Ⅰ）设在男生、女生中分别抽取m名和n名，则，6290015009001500sinAsinBsinCsin4解得：m60,n40.·····························································································2分所以b62sinB，c62sinC.····································································5分记抽取的总样本的平均数为，根据按比例分配分层随机抽样总样本平均数与各层样本平均数的关1所以SbcsinA182sinBsinC182sinBsin（B）ABC24高三数学试题答案第2页（共8页）22a2b2c25b16182sinB（cosBsinB）18sinBcosB18sin2B9sin2B99cos2B因为cosC，222ab3b4(b2)(8b)92sin（2B）9···················································································9分所以sinC1cos2C43b因为ABC是锐角三角形14(b2)(8b)所以SabsinC3bABC0B30B23b所以2又CB,所以2,所以B.···············10分43420C0B16342424b210b16，（b）···················································10分5532所以2B，所以sin（2B）1.········································11分1614444424由二次函数yx210x16的性质可得，当x5时，函数取最大值9；当x时，y.52548所以992sin（2B）92.所以S12····························································································12分45ABC法二：所以分18SABC929··················································································12ABC中，ACAB10BC6，所以点A的轨迹为以B，C为焦点，10为长轴长的椭圆（注：利用余弦定理，解出bc929，仅得出S的最大值，给9分）ABC的一部分.以BC中点为坐标原点，BC所在直线为x轴建立平面直角坐标系.选择②x2y2因为bc10，则c10b可得A点所在的椭圆为:1，如图································································6分2516b2c2a2cosA0不妨设A在x轴上方，坐标为A（x，y）2bc00222因为是锐角三角形，所以acb，ABCcosB0222bca2accosAa2b2c22bccosC02ab（bc）22bc3622222bcab（10b）3602bc即a2c2b236（10b）2b202222（）2642bc32abc36b10b012bcbc1634所以b········································································7分5532327110，（bc）225254高三数学试题答案第3页（共8页）当且仅当时，即点在短轴端点时，取得最小值，此时角最大是锐角此时，由（1）可知FOAC,EOACO,所以FO平面AECbcAA2A,y04又EA平面AEC,所以FOEA.1Say12ABC0过作连接,又,所以平面2·····························································································8分OOGAE，GFOGOFOEAOFGGF平面OFG,所以EAGF,当与轴垂直时，即点在图中时，角为直角，此时16，148ABxAA1By0SABCay0525则OGF为二面角FAEC的平面角····································································8分16148当AC与x轴垂直时，即A点在图中A时，角C为直角，此时y，Say305ABC205····························································································································10分综上，A位于除去端点的弧A1A3上时，满足ABC是锐角三角形.116Say，（y4）············································································11分ABC2050OEOA6在RtEOA中，OGEAOEOA,OGEA548所以SABC1252264在RtFOG中，FGOGOF2·················································10分5548同理可得A在x轴下方时，S12，5ABCOG6则cosOGFFG448综上，S12·························································································12分5A