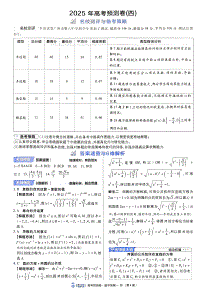
高三数学一、单选题1.已知全集,,,则( )A. B. C. D.2.命题“”是真命题的一个必要不充分条件是( )A. B. C. D.3.已知是定义在R上的奇函数,的图象关于对称,,则( )A. B.0 C.1 D.24.已知函数,则( )A.的最小正周期为B.为的一个极值点C.点是曲线的一个对称中心D.函数有且仅有一个零点5.在等比数列中,若,,则( )A. B. C.1 D.6.若,则( )A. B. C. D.7.已知分别是双曲线的左、右焦点,过作双曲线C的渐近线的垂线,垂足为P,且与双曲线C的左支交于点Q,若(O为坐标原点),则双曲线的离心率为( )A. B. C. D.8.已知为自然对数的底数,为函数的导数.函数满足,且对任意的都有,,则下列判断正确的是( )A. B.C. D.二、选择题:本大题共4小题,每小题5分,共计20分.每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,选对但不全得2分,有选错得0分.9.连续抛掷两次骰子,“第一次抛掷结果向上的点数小于3”记为事件,“第二次抛掷结果向上的点数是3的倍数”记为事件,“两次抛掷结果向上的点数之和为偶数”记为事件,“两次抛掷结果向上的点数之和为奇数”记为事件,则下列叙述中正确的是( )A.与互斥 B.C.与相互独立 D.与不相互独立10.已知函数,,使方程有4个不同的解:分别记为,其中,则下列说法正确的是( ).A. B.C. D.的最小值为1411.关于函数,则下列结论正确的有()A.是奇函数 B.的最小正周期为C.的最大值为 D.在单调递增12.已知函数,则( )A.B.若有两个不相等的实根,,则C.D.若,,均为正数,则二、填空题(本大题共4小题,每小题5分,共20分)13.已知命题“,”是假命题,则实数a取值范围是___.14.已知函数的定义域为,则实数a的取值范围为________.15.已知,则关于x的不等式的解集是______.16.已知定义在(0,+)上的函数f(x)满足:,若方程在(0,2]上恰有三个根,则实数k的取值范围是___________.四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知为等比数列的前n项和,若,,成等差数列,且.(1)求数列的通项公式;(2)若,且数列的前n项和为,证明:.18.(12分)在中,a,b,c分别为内角A,B,C的对边,.(1)求角A的大小;(2)若是锐角三角形,,求面积的取值范围.19.设函数,其中.曲线在点处的切线方程为.(1)确定,的值;(2)若,过点可作曲线的几条不同的切线?20.如图,在五面体中,底面四边形为正方形,平面平面.(1)求证:;(2)若,,,,求平面与平面所成的锐二面角的余弦值.21.设函数,其中在,曲线在点处的切线垂直于轴(Ⅰ)求a的值;(Ⅱ)求函数极值.22.在平面直角坐标系xOy中,曲线C的参数方程为(m为参数),以坐标点O为极点,x轴的非负半轴为极轴建立极坐标系,直线l的极坐标方程为ρcos(θ+)=1.(1)求直线l的直角坐标方程和曲线C的普通方程;(2)已知点M(2,0),若直线l与曲线C相交于P、Q两点,求的值. 1.B2.A3.A4.B5.A6.C7.B8.B9.ABC10.AC11AC12BCD【13题答案】【答案】【14题答案】【答案】【15题答案】【答案】【16题答案】【答案】17.(1)(2)证明见解析【分析】(1)首先列方程,求公比;其次,列方程,求首项;最后求出数列的通项公式;(2)求出,然后运用裂项相消法求出可得结论.【详解】(1)设数列的公比为q,由,,成等差数列可得,故,解得,由可得,解得,故,即数列的通项公式为.(2)由(1)可得,故.当时,取得最大值,当时,,故.18.(1)(2)【分析】(1)利用正弦定理结合两角和差化积公式转化条件得,进而求得解;(2)由题意,由正弦定理结合得,根据为锐角三角形求得,即可求得,即可得解.【详解】(1)由正弦定理得即又所以即又,,即,即又,,即(2)由题意得:,由正弦定理得:,又为锐角三角形,∴,故,∴,∴,从而.所以面积的取值范围是19【答案】(1),;(2)3条.【解析】【分析】(1)求,根据导数的几何意义可得,,即可求得,的值;(2)求出以及,设切点为,利用切点与点所在直线的斜率等于以及切点满足的解析式列方程,利用导数判断对应函数零点的个数即可求解.【详解】(1)由得,,因为曲线在点处的切线方程为,所以切线的斜率为,且故,(2)时,,,点不在的图象上,设切点为,则切线斜率,所以,即上式有几个解,过就能作出的几条切线.令,则,由可得或;由,可得,所以在单调递增,在单调递减,在单调递增,所以极大值为,极小值为,所以有三个零点,即过可作出的条不同的切线.20【答案】(1)证明见解析;(2).【解析】【分析】(1)证明平面,即得证;(2)以D为坐标原点,分别以,,所在直线分别为x,y,z轴建立空间直角坐标系,利用向量法求平面与平面所成的锐二面角的余弦值.【详解】证明:(1)在正方形中,,平面,平面,平面,又平面,且平面,.(2)四边形为正方形,,平面,平面,平面,,又,以D为坐标原点,分别以,,所在直线分别为x,y,z轴建立空间直角坐标系,如图所示,则,,,可知为平面一个法向量,设平面的一个法向量为,,则,令,,设平面与平面所成的锐二面角为,则,故平面与平面所成的锐二面角的余弦值为.【21题答案】【答案】(Ⅰ)(Ⅱ)极小值
吉林省梅河口市第五中学2024届高三上学期9月月考试题+数学+Word版含解析
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
湖北省荆州中学2023-2024学年高三上学期10月半月考 数学
2023-11-16 22:38
 4页
4页 -
湖北省腾云联盟2023-2024学年高三上学期8月联考数学答案
2023-11-16 22:38
 5页
5页 -
湖北省腾云联盟2023-2024学年高三上学期8月联考物理答案
2023-11-16 22:38
 3页
3页 -
湖北省腾云联盟2023-2024学年高三上学期8月联考 化学
2023-11-16 22:38
 8页
8页 -
湖北省腾云联盟2023-2024学年高三上学期8月联考 地理
2023-11-16 22:38
 5页
5页 -
湖北省荆州中学2023-2024学年高三上学期10月半月考 物理
2023-11-16 22:38
 6页
6页 -
湖北省腾云联盟2023-2024学年高三上学期8月联考 物理
2023-11-16 22:38
 6页
6页 -
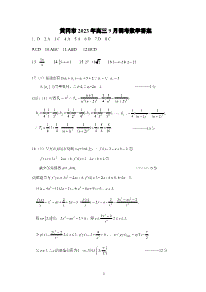
黄冈市2023年高三9月调考数学答案
2023-11-16 22:38
 4页
4页