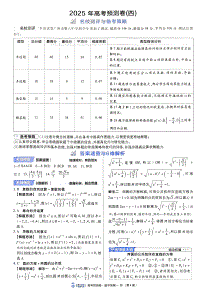
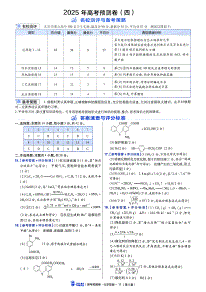
24届高三理科数学上期10月阶段性考试试卷本试卷分第I卷(选择题)和第II卷(非选择题)两部分，共150分，考试时间120分钟.第I卷一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1.已知复数z满足：zi1i（i为虚数单位），则||z()2A.B.1C.2D.222.已知集合A{x|2x0}，B{x|x21}，则AB()A.[2,1)B.[2,0](1,)C.(,0](1,)D.[2,1)3.抛物线C:y2mx过点(2,3)，则抛物线C的准线方程为()3333A.xB.xC.yD.y88884.为了得到函数yxcos(2)的图象，只要把函数yxcos(2)的图象上所有点()66A.向左平行移动个单位长度B.向右平行移动个单位长度66C.向左平行移动个单位长度D.向右平行移动个单位长度33xy225.已知F，F为双曲线C:1(a0,b0)的左、右焦点，以线段FF为直径的圆与12ab2212双曲线C的右支交于P、Q两点，若|PF12|3|PF|，其中O为坐标原点，则的离心率为()313A.B.3C.1D.31226.异速生长规律描述生物的体重与其它生理属性之间的非线性数量关系，通常以幂函数形式表示.比如，某类动物的新陈代谢率y与其体重x满足ykx，其中k和为正常数，该类动物某一个体在生长发育过程中，其体重增长到初始状态的16倍时，其新陈代谢率仅提高到初始状态的8倍，则为()1123A.B.C.D.42347.设等比数列{}an的前n项和为Sn，且有aa3225，S33，则{}an的公比为()1111A.或5B.2或C.或5D.2或25251{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}三、解答题(共70分，解答应写出文字说明、证明过程或演算步骤.)17.（12分）已知等差数列an的前n项和为Sn，且满足a1a3a515，S749.（1）求an的通项公式；n（2）若数列bn满足bann3，求bn的前项和Tn.18.（12分）如图，已知等腰直角三角形RBC，其中RBC90，RBBC2.点A､D分别是RB､RC的中点，现将RAD沿着边AD折起到PAD位置，使PAAB，连接PB､PC.（1）求证：BCPB；（2）求二面角ACDP的平面角的余弦值.19（12分）由“杂交水稻之父”袁隆平团队研发的晚稻品种“叁优一号”亩产为911．7公斤．在此之前，同一基地种植的早稻品种亩产为619．06公斤．这意味着双季亩产达到1530．76公斤，实现了“1500公斤高产攻关”的目标．在水稻育种中，水稻的不同性状对水稻的产量有不同的影响．某育种科研团队测量了株高(单位：cm)和穗长的数据，如下表(单位：株)：长穗短穗总计高杆341650低杆104050总计4456100（1）试判断能否在犯错概率不超过0.01的前提下认为株高和穗长之间有关系？n()adbc2(参考公式：K2，其中nabcd)(ab)(cd)(ac)(bd)PK2k0．100．050．0250．0100．0050．001k2．7063．8415．0246．6357．87910．828（2）把频率当成概率，在采样的稻田里随机抽取3株测量每穗总粒数，把抽取的低杆长穗株数记为X，求X的分布列和数学期望．3{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}xy2220.（12分）已知椭圆E:1(ab0)的一个顶点为A(0,1)，焦距为23．ab22（1）求椭圆E的方程；（2）过点P(2,1)作斜率为k的直线与椭圆E交于不同的两点B，C，直线AB，AC分别与x轴交于点M，N．证明：MN2||k为定值，并求出该值．21.（12分）设函数f(x)exlnx，（1）当x1时，判断方程f(x)e(x1)实根的个数，并说明原因；1ex2（2）若ae，有f()x1a，f(x2)a1，证明：e.x1x3cos22.（10分）在直角坐标系xoy中，曲线的参数方程为（为参数），以C1y3sin3坐标原点O为极点，以x轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为C2sin2．3(1)写出的极坐标方程和的普通方程；C1C25(2)设曲线C:(0)与，C的交点分别为M，N，求MN的值．3624{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}24届高三理科数学上期10月阶段性考试试卷答案一、单选题：共12道小题，每题5分,共60分.123456789101112CCABDDCADBBB二、填空题：共4道小题，每题5分,共20分.13.2414.6815.116.①④三、解答题：共5道大题，共70分.17.（12分）解：（1）因为a135a+a+=15，S7=49，3ad61+=5,所以所以a=1，d=2，所以ann=+1−(1)=2−21.72ad14+=9,n23n（2）由题可知bnn=−(21)3，所以Tnn=++++−133353(21)3①，234n+13133353(21)3Tnn=++++−②，234nn+1①-②得，−=+++++−−21323232323(21)3Tnn2323−21n+=+3−−(21)3nn+1=−(+22)n−36n+1，13−n+1故Tnn=−(1)+33.118.（12分）解：（1）∵点A､D分别是RB､RC的中点，∴ADBC//，ADB=C.2又∵=RBC90，RAD沿着边AD折起到PAD位置，∴=PADRADRBC==90.∴PAAD⊥.∴PABC⊥，∵BCAB⊥，PAABA=，∴BC⊥平面PAB.∵PB平面PAB，∴BCPB⊥.（2）取RD的中点F，连接AF､PF.∵RAAD==1，∴AF⊥RC.∵APAR⊥，APAD⊥，∴AP⊥平面RBC.∵RC平面RBC，∴RCAP⊥，∵AF=APA，∴RC⊥平面PAF.∵PF平面，∴RCPF⊥.∴AFP是二面角ACDP−−的平面角.112在Rt△RAD中，AF=RD=RA22+AD=，在Rt△PAF中，2222226AF23PFPAAF=+=，cosAFP===.2PF632∴二面角的平面角的余弦值是3.3100(3440−1610)219．（12分）解：(1)根据2×2列联表中的数据，可得K2=5050445623.3776.635，故能在犯错误的概率不超过0．01的前提下认为株高和穗长之间有关系．(2)记“在采样的稻田里抽出低杆长穗稻株”为事件A，1011则PA()==，所以XB~3,．X的所有可能取值为0，1，2，3，10010101{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}令Fxfexfx()()()1=−−，而Fx()=eexexexxlnln1−−=eeexexexx+−−()ln1，1当x时，ln1x−，eeexx−0，ex−10，eexexxxe+(e−e)(−1)−1=e−10，取xx=1，即Fx()01，x2则fexfxfx()()1()112+=，即ex12x，也即e.x1x=3cosx=3cos①22.（10分）解：（1）因为，则①2②得的普通方程+C1y=+3sin3y−=33sin②x=cos为：22，即22根据可知的极坐标方程为：xy+−(=39)xyy+−=60C1y=sin=6sin；13，的普通方程为：.sin2sincos2−=−=C234xy0−+=3225π5π（2）设，MM,NN,665π5，，.M==6sinπ3NNsinπ−==22MNOMON=−=−=MN16633{#{QQABYQ4AoggAAAAAAQhCUwVACgAQkAECCAoGRAAAMAAAwBFABAA=}#}