衡水泰华中学2022-2023高三数学暑假作业第八套组编人:魏然审核人:魏然姓名:得分:家长签字:立体几何第8套在SA上,且SB=2BA,则过点B的平面被该球O截得的截面面积的最小值为()A.27πB.32πC.45πD.81π一.选择题(共8小题)7.《九章算术》是我国古代著名数学经典,其中对勾股定理的论述,比西方早一千多年,其中有这1.已知m,n是空间中两条不同的直线,α,β为空间中两个不同的平面.样一个问题:“今有圆材埋在壁中,不知大小;以锯锯之,深一寸,锯道长一尺,问径几何?”①若m⊂α,α⊥β,则m⊥β;其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深1寸,锯道②若m⊥α,m∥n,n∥β,则α⊥β;长1尺,问这块圆柱形木料的直径是多少?长为0.5丈的圆柱形木材部分镶嵌在墙体中,截面图③若m⊥β,n⊥β,n⊥α,则m⊥α;如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木④若m⊥α,m⊥n,则n∥α;材镶嵌墙内部分的体积约为()(注:一丈=10尺=100寸,π≈3.14,sin22.5°≈)⑤若α∥β,m⊂α,n⊂β,则m∥n.则以上说法正确的是()A.300立方寸B.305.6立方寸A.①⑤B.②③④C.②③D.①②④⑤C.310立方寸D.316.6立方寸2.在底面半径为1的圆锥中,若该圆锥侧面展开图的面积是2π,则该圆锥的体积为()A.B.C.D.3.在正三棱锥A﹣BCD中,侧棱长为2,底面边长为2,则三棱锥A﹣BCD的公外众接号球【的阿体积为()第7题第8题图A.36πB.24πC.12πD.6π8.在棱长为2的正方体ABCD﹣A1B1C1D1中,E是正方形BB1C1C的中心,M为C1D1的中点,4.已知四面体ABCD内接于半径为R的球O内,BC=AB=3,∠BAC=,若球心O过A1M的平面α与直线DE垂直,则平面α截正方体ABCD﹣A1B1C1D1所得的截面面积为()到平面ABC的距离为,则四面体ABCD体积的最大值为()A.2B.2C.D.3A.2B.C.D.二.多选题(共4小题).对于两条不同直线,和两个不同平面,,则下列说法中正确的是()5.已知某正三棱锥的底面边长为4,侧面与底面所成二面角的余弦值为,球O1为该三棱锥的内9mnαβA.若m⊥α,n⊥α,则m∥n切球.球O2与球O1相切,且与该三棱锥的三个侧面也相切,则球O2与球O1的表面积之比为B.若m⊂α,n⊂α,m∥β,n∥β,则α∥β()C.若α⊥β,m⊂α,则m⊥βA.B.C.D.D.若α⊥β,m⊥β,m⊄α,则m∥α6.已知圆锥SO的顶点和底面圆周均在球O的球面上,且该圆锥的高为8.母线SA=12,点B1明德求是追求卓越衡水泰华中学2022-2023高三数学暑假作业第八套组编人:魏然审核人:魏然姓名:得分:家长签字:10.如图,在直三棱柱ABC﹣A1B1C1中,AC=BC=CC1=6,AC⊥BC,E、E分别为BB1,A1C113.如图,AOB是用斜二测画法得到的AOB的直观图,其中OA3,OB2,则AB的长度中点,过点A、E、F作三棱柱的截面α,则下列结论中正确的是()为______.A.BC1∥αB.直线BC与直线AF所成角为90°C.若α交B1C1于M,则FM=5D.α将三棱柱ABC﹣A1B1C1分成体积较大部分和体积较小部分,其中较大部分的体积为76第13题图第15题图14.已知在棱长为1的正方体ABCD﹣A1B1C1D1,中,E为平面D1A1AD的中心,F为CE的中点,过F作FM⊥CE交D1C于点M,则三棱锥M﹣DEF体积为.15.如图,平面ABC⊥平面BCDE,四边形BCDE为矩形,BE=2,BC=4,△ABC的面积为2,点P为线段DE上一点,当三棱锥P﹣ACE的体积为时,=.第10题图第11题图SABCABACBC23SBSCSBC11.在正方体ABCD﹣A1B1C1D1中,AB=4,E,F分别为BB1,CD的中点,P是BC1上的动点,16.已知三棱锥中,,,平面平面ABC,则三棱锥则()的外接球的表面积为______.A.A1F⊥平面AD1E四.解答(共6个小题)B.平面AD1E截正方体ABCD﹣A1B1C1D1的截面面积为1817.如图,已知AF平面ABCD,四边形ABEF为矩形,四边形ABCD为直角梯形,DAB90,C.三棱锥P﹣AD1E的体积与P点的位置有关ABCD,ADCD2,AB4.D.过AE作正方体ABCD﹣A1B1C1D1的外接球的截面,所得截面圆的面积的最小值为5π12.把正方形ABCD沿对角线BD折成直二面角A﹣BD﹣C,则下列四个结论中正确的结论是()A.AC⊥BDB.△ACD是等边三角形(1)求证:AF∥平面BCE;C.AB与平面CBD成60°角(2)求证:平面ACF平面BCE.D.AB与CD所成角为45°三.填空题(共4小题)明德求是追求卓越衡水泰华中学2022-2023高三数学暑假作业第八套组编人:魏然审核人:魏然姓名:得分:家长签字:18.如图,正方体ABCDA1BC11D1的棱长为1,线段BD11上有两个不同的动点E,F.20.如图,在圆柱OO1中,四边形ABCD是其轴截面,EF为O1的直径,且EF⊥CD,AB=2,BCa(a0).(1)求证:EF//平面ABCD;(1)求证:BE=BF;(2)求证:ACBE;(2)若直线AE与平面DEF所成角为,求三棱锥ABEF的体积.(3)二面角AEFB的大小是否为定值,若是,求出其余弦值;若不是,说明理由.419.如图,直四棱柱中ABCDA1BC11D1中,AB//CD,ADBCCD2,AB4,AA13,设M为BC11的中点.(1)求四棱柱ABCDA1BC11D1的表面积;求证:CD//面;(2)1AMCV1(3)连接AC1,记C1AMC三棱锥的体积为V1,四棱柱ABCDA1BC11D1的体积为V2,求的值.V2明德求是追求卓越衡水泰华中学2022-2023高三数学暑假作业第八套组编人:魏然审核人:魏然姓名:得分:家长签字:21.如图,AB是O的直径,C是圆周上异于AB,的点,P是平面ABC外一点,且22.图1是直角梯形ABCD,AB∥CD,D90,四边形ABCE是边长为2的菱形,并且BCE60,PAPBPC3.以BE为折痕将BCE折起,使点C到达C1的位置,且AC16,如图2.(1)求证:平面PAB平面ABC;(2)若AB2,点D是O上一点,且与C在直径AB同侧,DABABC60.(1)求证:平面BC1E平面ABED;设平面平面PCDl,求证:l//CD;①PAB15(2)在棱DC1上是否存在点P,使得P到平面ABC1的距离为?若存在,求出直线EP与平面②求二面角DlA的正切值.5ABC所成角的正弦值1.明德求是追求卓越
2024新高考衡水内部卷数学第八套题
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
2024新高考衡水内部卷数学第九套圆锥曲线
2023-11-29 15:29
 4页
4页 -
2024新高考衡水内部卷数学假期7答案
2023-11-29 15:29
 7页
7页 -
2024新高考衡水内部卷数学假期作业1
2023-11-29 15:29
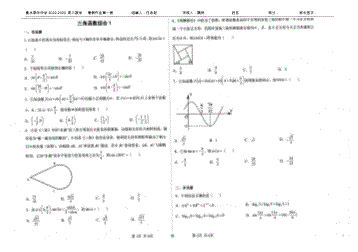 3页
3页 -
2024新高考衡水内部卷数学18答案
2023-11-29 15:29
 3页
3页 -
2024新高考衡水内部卷数学22
2023-11-29 15:29
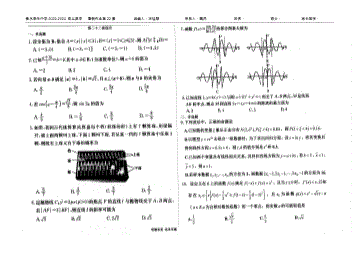 4页
4页 -
2024新高考衡水内部卷数学答案
2023-11-29 15:29
 6页
6页 -
2024新高考衡水内部卷数学第10套假期作业之圆锥曲线答案
2023-11-29 15:29
 8页
8页 -
2024新高考衡水内部卷数学立体几何第八套答案
2023-11-29 15:29
 6页
6页













