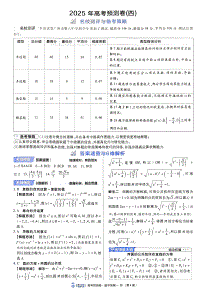
广西武鸣高中2024届高三(上)开学调研测试题数学一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知集合Axx2,Bxxx30,则AB()A.{xx2或x3}B.x2x0C.x2x3D.x0x22.已知复数z满足z1ii3(i是虚数单位),则z的虚部是()1111A.iB.iC.D.22223.记Sn为等差数列an的前n项和.若a4a524,S648,则a9()A.4B.24C.30D.324.如图,某同学为测量鹳雀楼的高度MN,在鹳雀楼的正东方向找到一座建筑物AB,高约为37m,在地面上点C处(B,C,N三点共线)测得建筑物顶部A,鹳雀楼顶部M的仰角分别为30°和45°,在A处测得楼顶部M的仰角为15°,则鹳雀楼高度约为()A.91mB.74mC.64mD.52mx2y25.已知椭圆C:1(ab0)的左、右顶点分别为A1,A2,且以线段A1A2为直径a2b2xy的圆与直线20相切,则C的离心率为()ab6321A.B.C.D.33334x6.已知函数f(x)=,则()2+4xA.f0.1f0.2B.函数fx有一个零点11C.函数fx是偶函数D.函数fx的图象关于点,对称2227.设fx是定义在R上的奇函数,且当x0时,fx=x,若对任意的xt,t2,不等式fxt2fx恒成立,则实数t的取值范围是()A.2,B.2,C.0,2D.2,12,38.武术是中国的四大国粹之一,某武校上午开设文化课,下午开设武术课,某年级武术课有太极拳、形意拳、长拳、兵器四门,计划从周一到周五每天下午排两门课,每周试卷第1页,共4页{#{QQABCYaEogCAAhBAABgCEQWQCAGQkAAACKgOxFAIMAABSAFABAA=}#}太极拳和形意拳上课三次,长拳和兵器上课两次,同样的课每天只上一次,则排课方式共有()A.19840种B.16000种C.31360种D.9920种二、选择题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分)9.若ab,则()ab3311A.lnab0B.33C.ab0D.ab10.下列命题为真命题的有()12A.若随机变量X的方差为,则D(5X2)1425B.已知y关于x的回归直线方程为yˆ0.30.7x,则样本点(2,3)的残差为1.91C.若随机变量XN,2,且P(X4)P(X2)p,则P2X1p2D.根据分类变量X与Y的成对样本数据,计算得到23.712,根据0.05的独立性检验(P(23.841)0.05),有95%的把握认为X与Y有关11.已知O为坐标原点,抛物线C:y22pxp0的准线方程为x=1,过焦点F的直线l交抛物线C于A,B两点,则()A.若AF5,则OA42B.若AB8,则直线l的斜率为1C.2AFBF322D.OAB面积的最小值为212.点A,B在以PC为直径的球O的表面上,且ABBC,ABBC2,已知球O的表面积是12π,设直线PB和AC所成角的大小为,直线PB和平面PAC所成角的大小为,四面体PABC内切球半径为r,下列说法中正确的个数是()1A.BC平面PABB.平面PAC平面ABCC.rD.sincos2三、填空题(本题共4小题,每小题5分,满分20分)52213.在x的展开式中,x的系数为.(用数字作答)x14.已知向量a2,5,bcos,sin2,且a//b.则sin的值为.15.已知A,B两城市的距离是100km,根据交通法规,两城市之间的公路车速应限制在50~100km/h,假设油价是6元/L,以xkm/h的速度行驶时,汽车的耗油率为x23L/h,其它费用是36元/h.为了这次行车的总费用最少,那么最经济的车速360是km/h(精确到1km/h,参考数据103.162)16.已知函数fxex2lnx,gxa2x2x2lna(a1),若fx的图象与gx的图象在1,上恰有两对关于x轴对称的点,则实数a的取值范围是.试卷第2页,共4页{#{QQABCYaEogCAAhBAABgCEQWQCAGQkAAACKgOxFAIMAABSAFABAA=}#}四、解答题(共6小题,其中17题10分,其他题12分,满分70分)17.公差不为零的等差数列an的前n项和为Sn,若S39,且a1,a2,a5成等比数列.(Ⅰ)求数列an的通项公式;(Ⅱ)设bnan是首项为1,公比为2的等比数列,求数列bn的通项公式及其前n项和Tn.18.某研究机构随机抽取了新近上映的某部影片的120名观众,对他们是否喜欢这部影片进行了调查,得到如下数据(单位:人):喜欢不喜欢合计男性403070女性351550合计7545120根据上述信息,解决下列问题:(1)根据小概率值0.10的独立性检验,分析观众喜欢该影片与观众的性别是否有关;(2)从不喜欢该影片的观众中采用分层抽样的方法,随机抽取6人.现从6人中随机抽取2人,若所选2名观众中女性人数为X,求X的分布列及数学期望.2nadbc附:2,其中nabcd.abcdacbd0.150.100.050.0100.001x2.0722.7063.8416.63510.82819.已知在四棱锥PABCD中,AB4,BC3AD5,DABABCCBP90,PACD,E为CD的中点.(1)证明:平面PCD平面PAE;(2)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求二面角PCDA的正弦值.试卷第3页,共4页{#{QQABCYaEogCAAhBAABgCEQWQCAGQkAAACKgOxFAIMAABSAFABAA=}#}20.某工厂购进一批加工设备,由于该设备自动模式运行不稳定,因此一个工作时段内1会有的概率出现自动运行故障.此时需要1名维护人员立刻将设备切换至手动操控模4式,并持续人工操作至此工作时段结束,期间该维护人员无法对其他设备进行维护.工厂在每个工作时段开始时将所有设备调至自动模式,若设备的自动模式出现故障而得不到维护人员的维护,则该设备将停止运行,且每台设备运行的状态相互独立.(1)若安排1名维护人员负责维护3台设备,求这3台设备能顺利运行至工作时段结束的概率;(2)设该工厂有甲、乙两个车间.甲车间有6台设备和2名维护人员,将6台设备平均分配给2名维护人员,每名维护人员只负责维护分配给自己的3台设备;乙车间有7台设备和2名维护人员,7台设备由这2名维护人员共同负责维护.若用车间所有设备顺利运行至工作时段结束的概率来衡量生产的稳定性,试比较甲、乙两个车间生产稳定性的高低.x2y221.已知双曲线E:1a0,b0的离心率为3,点P2,2在双曲线E上.a2b2(1)求E的方程;(2)过点M1,0的直线l与双曲线E交于A,B两点(异于点P).设直线BC与x轴垂直且交直线AP于点C,若线段BC的中点为N,判断:P,M,N三点是否共线?并说明理由.22.设函数fxexax,其中aR.(1)讨论函数f(x)在[1,)上的极值;xx(2)若函数f(x)有两零点x,xxx,且满足121,求正实数的取值范围.12121试卷第4页,共4页{#{QQABCYaEogCAAhBAABgCEQWQCAGQkAAACKgOxFAIMAABSAFABAA=}#}
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 数学
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 化学答案
2023-11-18 09:13
 8页
8页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 历史
2023-11-18 09:13
 6页
6页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 政治
2023-11-18 09:13
 6页
6页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 英语答案
2023-11-18 09:13
 8页
8页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 英语
2023-11-18 09:13
 12页
12页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 数学答案
2023-11-18 09:13
 8页
8页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 生物
2023-11-18 09:13
 9页
9页 -
广西南宁市武鸣高级中学2023-2024学年高三上学期开学考试 物理
2023-11-18 09:13
 6页
6页