2024年郑州市高中毕业年级第三次质量预测数学评分参考一、单选题题号12345678答案ADABDCAC二、多选题题号91011答案BCACDACD三、填空题11112.;13.26;14.()n1.222四、解答题15.(13分)12345(1)由已知可得,x3,56.45.55.04.83.8y5.1,………………2分5由题可列下表:-2-1012xix1.30.4-0.1-0.3-1.3yiy555,22(xix)(yiy)5.9(xix)10,(yiy)3.64.i1i1i15(xx)(yy)ii5.95.9ri10.98.……………………5分552236.46(xix)(yiy)i1i1(2)由(1)知,y与x的相关系数r0.98,r接近1,所以y与x之间具有极强的线性相关关系,可用线性回归模型进行描述.………………8分学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司1{#{QQABKY4EggiAQpBAABgCQQEACgEQkAGACIoOgBAIIAAASBFABCA=}#}5(xx)(yy)ii5.9()由()知,i1,………………分31b50.599210(xix)i1………………分aybx5.1(0.59)36.87.10所求经验回归方程为y0.59x6.87.………………11分(3)令x8,y2.15,预测2024年的酸雨区面积占国土面积的百分比为2.15%.…13分16.(15分)2x2x解(1)若a2,则f(x)ex,f(x)2e1.………………1分又f(1)e21.故所求切线方程为y(e21)(2e21)(x1)即y(2e21)xe2.………………4分………………分(2)由题f(x)aeax1.51。当a0时,f(x)0,f(x)在R上单调递减,又f(0)10,f(1)ea10.………………分f(x)存在一个零点,此时f(x)零点个数为1.7lnalna2。当a0时,令f(x)0得x,令f(x)0得x,aalnalna则f(x)在(,)上单减,在(,)上单增.aalna1lna………………分f(x)的最小值为f().9aa1………………分I)当a时,f(x)的最小值为0,此时f(x)有一个零点.11e1………………分Ii)当a时,f(x)的最小值大于0,此时f(x)没有零点.13e1Iii)当0a时,f(x)的最小值小于0,f(1)ea10,elna1lnaf()<0,x时,f(x).此时f(x)有两个零点.aa11综上,当a0或a时,f(x)有一个零点;当0a时,f(x)有两个零点;ee1………………分当a时,f(x)没有零点.15e学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司2{#{QQABKY4EggiAQpBAABgCQQEACgEQkAGACIoOgBAIIAAASBFABCA=}#}17.(15分)(1)证明:如图,在等腰梯形ABB1A1中,连接BA1,1又∵AA1=A1B1=BB1=AB=1,可以解得BA1=3,2222在三角形BAA1中,AA1+BA1=AB,∴BA1⊥AA1,……………2分又∵,且,平面ABB1A1平面ABC平面ABB1A1平面ABCABACAB,且AB平面ACCA11,∴⊥平面,∴⊥.………………分ACABB1A1BA1AC4又∵AAACA,且AC,AA平面ACCA1111,∴BA1⊥平面ACC1A1.………………5分(2)由(1)可知,VV,A1ABCCABA1113∴13AC,AC3.………………7分322∴以A为原点,以AC,AB为x,y轴,建立如图所示的空间直角坐标系A﹣xyz.1333可得:B(0,2,0),C(3,0,0),A(0,,),B(0,,).12212233易知平面ACC1A1的一个法向量为BA(0,,),………………9分12213设平面BCC1B1的法向量为n(,xyz,),又∵BB(0,,),BC(3,2,0),12213nBByz0,由122nBC3x2y0,令z3,解得平面BCC1B1的一个法向量为n(2,3,3),………………12分3∴cosBA,n.………………14分143∴平面ACC1A1与平面BCC1B1的夹角的余弦值为.………………15分418.(17分)b2343解:(1)由题意得e21,将P(2,3)代入椭圆方程得1,联立方程组,a24a2b22a16x2y2解得,∴椭圆的方程为.………………………………4分21b4164(2)直线AP与椭圆C相切.………………5分学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司3{#{QQABKY4EggiAQpBAABgCQQEACgEQkAGACIoOgBAIIAAASBFABCA=}#}理由如下:x46设A(x,0),由AA:AAHA:HA,得,解得x8,此时A(8,0),…6分2121x423直线AP的方程为y(x8),…………7分63y(x8),62联立直线AP与椭圆C消y得,x4x40,解得x2.x2y21,164∴直线AP与椭圆C相切.…………10分(3)设T(8,t),由三点共线,得y1tT(8,tMxyA),(1,1),1(4,0),x144由三点共线,得y2tT(8,tNxy),(2,2),A2(4,0),x2412y(x4)x2y2y21y21得123,又∵1,得1,1,y(x4)221164x1164(xx14)(14)4(x4)(x4)得1212,y1y2即xx124(xx12)12yy12160.①设直线MN的方程为xmyn,22即(m12)y1y2(mn4m)(y1y2)n8n160.…………12分xmyn,222联立直线MN与椭圆Cx2y2消x得(m4)y2mnyn160,1,1642mnyy,12m24则有②…………14分n216yy,12m24将②式代入①式,得n22n80,解得n4(舍)或n2.∴直线MN经过定点(-2,0).…………17分19.(17分)学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司4{#{QQABKY4EggiAQpBAABgCQQEACgEQkAGACIoOgBAIIAAASBFABCA=}#}xcos3sin,44…………分(1)由题可设所求点的坐标为(x,y),由2ysin3cos,446262…………………………4分得所求点的坐标为(,).22………分(2)设曲线xy1上任意一点(x,y)在旋转角是的旋转变换下所得点坐标为(x,y).642xxcosysin,x(xy),442……………………分则即82yxsinycos,y(xy),442得(y)2(x)22xy2,22yx……………………分所求曲线方程为1.1022(3)由题点B(1,1)在旋转角是的旋转变换下所得的点为B(0,2).4设A,C在旋转角是的旋转变换下所得的点分别为A和C.4y2x2设曲线xy1在旋转角是的旋转变换下所得曲线为M,则M方程为1.422则B是曲线M的下顶点.……………分由题,ABC为等边三角形,ABC的面积即为ABC的面积.12设ABC的边长为t(t0),由双曲线的对称性:t3当A和C同在曲线M的下支时,则A(,t2),22……………………分代入M的方程得t无解.14t3当A和C同在曲线M的上支时,则A(,t2),22代入M的方程得t26.ABC的面积为63.……………………分综上所述,ABC的面积为63.17学科网(北京)股份有限公司学科网(北京)股份有限公司学科网(北京)股份有限公司5{#{QQABKY4EggiAQpBAABgCQQEACgEQkAGACIoOgBAIIAAASBFABCA=}#}
2024届河南省郑州市高中毕业年级第三次质量预测数学答案
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
2024届河南省郑州市高中毕业年级第三次质量预测数学试卷
2024-05-10 21:21
 6页
6页 -
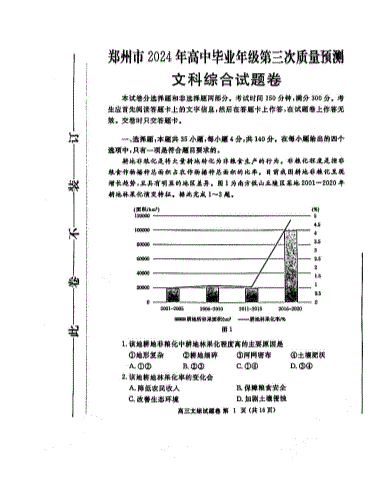
2024届河南省郑州市高中毕业年级第三次质量预测文综试题
2024-05-10 21:21
 16页
16页 -
2024届河南省郑州市高中毕业年级第三次质量预测(三模)英语试题
2024-05-10 21:21
 14页
14页 -
山东省菏泽市2024年高三二模考试历史答案
2024-05-10 21:21
 3页
3页 -
山东省菏泽市2024年高三二模考试英语试题
2024-05-10 21:21
 18页
18页 -
山东省菏泽市2024年高三二模考试历史试题
2024-05-10 21:21
 4页
4页 -
2024届四川省南充市高三下学期三模考试语文答案
2024-05-10 21:21
 4页
4页 -
2024届四川省南充市高三下学期三诊考试政治答案
2024-05-10 21:21
 3页
3页













