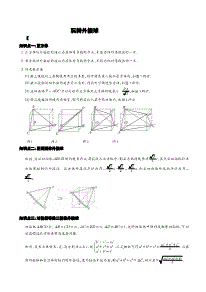
玩转外接球、内切球、棱切球【考点预测】知识点一:正方体、长方体外接球1.正方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．2.长方体的外接球的球心为其体对角线的中点，半径为体对角线长的一半．3.补成长方体(1)若三棱锥的三条侧棱两两互相垂直，则可将其放入某个长方体内，如图1所示．(2)若三棱锥的四个面均是直角三角形，则此时可构造长方体，如图2所示．PA(3)正四面体P-ABC可以补形为正方体且正方体的棱长a=，如图3所示．2(4)若三棱锥的对棱两两相等，则可将其放入某个长方体内，如图4所示图1图2图3图4知识点二:正四面体外接球2如图，设正四面体ABCD的的棱长为a，将其放入正方体中，则正方体的棱长为a，显然正四面体和正2236方体有相同的外接球．正方体外接球半径为R=a⋅=a，即正四面体外接球半径为R=2246a．4知识点三:对棱相等的三棱锥外接球四面体ABCD中，AB=CD=m，AC=BD=n，AD=BC=t，这种四面体叫做对棱相等四面体，可以通过构造长方体来解决这类问题．b2+c2=m2m2+n2+t2如图，设长方体的长、宽、高分别为a,b,c，则a2+c2=n2，三式相加可得a2+b2+c2=,而显2a2+b2=t2222Ra2+b2+c2=4R2R=m+n+t然四面体和长方体有相同的外接球，设外接球半径为，则，所以8．知识点四:直棱柱外接球如图1，图2，图3，直三棱柱内接于球(同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形)图1图2图3第一步：确定球心O的位置，O1是ΔABC的外心，则OO1⊥平面ABC；11第二步：算出小圆O的半径AO=r，OO=AA=h(AA=h也是圆柱的高)；1112121222222h22h第三步：勾股定理：OA=OA+OO⇒R=+r⇒R=r+，解出R1122知识点五:直棱锥外接球如图，PA⊥平面ABC，求外接球半径．解题步骤：第一步：将ΔABC画在小圆面上，A为小圆直径的一个端点，作小圆的直径AD，连接PD，则PD必过球心O；第二步：O1为ΔABC的外心，所以OO1⊥平面ABC，算出小圆O1的半径O1D=r(三角形的外接圆直径abc1算法：利用正弦定理，得===2r)，OO=PA；sinAsinBsinC12第三步：利用勾股定理求三棱锥的外接球半径：①(2R)2=PA2+(2r)2⇔2R=PA2+(2r)2；22222②R=r+OO1⇔R=r+OO1．知识点六:正棱锥与侧棱相等模型r2+h21.正棱锥外接球半径：R=．2h2.侧棱相等模型：如图，P的射影是ΔABC的外心⇔三棱锥P-ABC的三条侧棱相等⇔三棱锥P-ABC的底面ΔABC在圆锥的底上，顶点P点也是圆锥的顶点．解题步骤：第一步：确定球心O的位置，取ΔABC的外心O1，则P,O,O1三点共线；第二步：先算出小圆O1的半径AO1=r，再算出棱锥的高PO1=h(也是圆锥的高)；r2+h2第三步：勾股定理：OA2=OA2+OO2⇒R2=(h-R)2+r2，解出R=．112h知识点三:侧棱为外接球直径模型方法：找球心，然后作底面的垂线，构造直角三角形．知识点四:共斜边拼接模型如图，在四面体ABCD中，AB⊥AD，CB⊥CD，此四面体可以看成是由两个共斜边的直角三角形拼接而形成的，BD为公共的斜边，故以“共斜边拼接模型”命名之．设点O为公共斜边BD的中点，根据直角三角形斜边中线等于斜边的一半的结论可知，OA=OC=OB=OD，即点O到A，B，C，D四点的距离相等，故点O就是四面体ABCD外接球的球心，公共的斜边BD就是外接球的一条直径．知识点五:垂面模型如图1所示为四面体P-ABC，已知平面PAB⊥平面ABC，其外接球问题的步骤如下：(1)找出△PAB和△ABC的外接圆圆心，分别记为O1和O2．(2)分别过O1和O2作平面PAB和平面ABC的垂线，其交点为球心，记为O．(3)过O1作AB的垂线，垂足记为D，连接O2D，则O2D⊥AB．(4)在四棱锥A-DO1OO2中，AD垂直于平面DO1OO2，如图2所示，底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径．图1图2知识点六:最值模型这类问题是综合性问题，方法较多，常见方法有：导数法，基本不等式法，观察法等知识点七:二面角模型如图1所示为四面体P-ABC，已知二面角P-AB-C大小为α，其外接球问题的步骤如下：(1)找出△PAB和△ABC的外接圆圆心，分别记为O1和O2．(2)分别过O1和O2作平面PAB和平面ABC的垂线，其交点为球心，记为O．(3)过O1作AB的垂线，垂足记为D，连接O2D，则O2D⊥AB．(4)在四棱锥A-DO1OO2中，AD垂直于平面DO1OO2，如图2所示，底面四边形DO1OO2的四个顶点共圆且OD为该圆的直径．知识点八:坐标法对于一般多面体的外接球，可以建立空间直角坐标系，设球心坐标为O(x,y,z)，利用球心到各顶点的距离相等建立方程组，解出球心坐标，从而得到球的半径长．坐标的引入，使外接球问题的求解从繁琐的定理推论中解脱出来，转化为向量的计算，大大降低了解题的难度．知识点九:圆锥圆柱圆台模型1.球内接圆锥如图1，设圆锥的高为h，底面圆半径为r，球的半径为R．通常在△OCB中，由勾股定理建立方程来计算R．如图2，当PC>CB时，球心在圆锥内部；如图3，当PC接球的半径为R，三者之间满足+r2=R2．23.球内接圆台r2-r2-h22R2=r2+21，其中r,r,h分别为圆台的上底面、下底面、高．22h12知识点四:锥体内切球3V方法：等体积法，即R=体积S表面积知识点五:棱切球方法：找切点，找球心，构造直角三角形【题型归纳目录】题型一：正方体、长方体模型题型二：正四面体模型题型三：对棱相等模型题型四：直棱柱模型题型五：直棱锥模型题型六：正棱锥与侧棱相等模型题型七：侧棱为外接球直径模型题型八：共斜边拼接模型题型九：垂面模型题型十：最值模型题型十一：二面角模型题型十二：坐标法模型题型十三：圆锥圆柱圆台模型题型十四：锥体内切球题型十五：棱切球【典例例题】题型一:题型一：正方体、长方体模型例1.(2022·陕西安康·高二期末(理))长方体的长，宽，高分别为3，2，1，其顶点都在球O的球面上，则球O的体积为(       )A.43πB.12πC.48πD.323π例2.(2022·全国·高一阶段练习)已知三棱锥P-BCD中，BC⊥CD，PB⊥底面BCD，BC=1，PB=CD=2，则该三棱锥的外接球的体积为(       )79A.πB.π422725C.πD.π8932例3.(2022·北京市第三十五中学高一阶段练习)已知正方体外接球的体积是π，那么正方体的体对角3线等于(       )234243A.B.4C.D.．333例4.(2022·黑龙江·勃利县高级中学高一期中)据《九章算术》记载，“鳖臑”为四个面都是直角三角形的三棱锥．如图所示，现有一个“鳖臑”，PA⊥底面ABC，AB⊥BC，且PA=AB=BC=2，三棱锥外接球表面积为(       )A.10πB.12πC.14πD.16π例5.(2022·河北·高一期中)《九章算术》中将底面为长方形且有一条侧棱与底面垂直的四棱锥称为“阳马”．现有一“阳马”P-ABCD，PA⊥平面ABCD，AB=4，△PAD的面积为4，则该“阳马”外接球的表面积的最小值为(       )A.24πB.28πC.32πD.36π例6.(2022·河南·模拟预测(文))在三棱锥A-BCD中，已知AC⊥平面BCD，BC⊥BD，且AC=3，BC=2，BD=5，则该三棱锥外接球的表面积为(       )A.12πB.7πC.9πD.8π题型二:正四面体模型例7.(2022·全国·高三专题练习(理))棱长为a的正方体内有一个棱长为x的正四面体，且该正四面体可以在正方体内任意转动，则x的最大值为(          )1336A.aB.aC.aD.a2263例8.(2022·河南·西平县高级中学模拟预测(理))一个正四面体的棱长为2，则这个正四面体的外接球的体积为(       )A.6πB.2πC.3πD.22π例9.(2022·贵州师大附中高二开学考试(理))已知正四面体的棱长为2，则其外接球的表面积为(     )A.4πB.6πC.8πD.10π例10.(2022·河北·石家庄二中一模(理))如图所示，正四面体ABCD中，E是棱AD的中点，P是棱AC上一动点，BP+PE的最小值为14，则该正四面体的外接球表面积是(       )A.12πB.32πC.8πD.24π例11.(2022·贵州·凯里一中高二期末(理))我们将四个面均为正三角形的四面体称为“正四面体”，在正四面体ABCD中，E,F分别为棱AB,CD的中点，当EF=2时，四面体ABCD的外接球的表面积为()A.12πB.4πC.3πD.6π例12.(2022·全国·高三专题练习)金刚石是碳原子的一种结构晶体，属于面心立方晶胞(晶胞是构成晶体的最基本的几何单元)，即碳原子处在立方体的8个顶点，6个面的中1心，此外在立方体的对角线的处也有4个碳原子，如图所示(绿色4球)，碳原子都以共价键结合，原子排列的基本规律是每一个碳原子的周围都有4个按照正四面体分布的碳原子．设金刚石晶胞的棱长为a，则正四面体SPQR的棱长为__________；正四面体SPQR的外接球的体积是__________．题型三:对棱相等模型例13.(2022•让胡路区校级模拟)在四面体ABCD中，若AB=CD=3，AC=BD=2，AD=BC=5，则四面体ABCD的外接球的表面积为( )A.2πB.4πC.6πD.8π例14.已知四面体ABCD中，AB=CD=5，BC=AD=10，AC=BD=13，若该四面体的各个顶点都在同一球面上，则此球的表面积为( )A.42πB.43πC.14πD.16π例15.如图，在三棱锥P-ABC中，PA=BC=3，PB=AC=2，PC=AB=5，则三棱锥P-ABC外接球的体积为( )A.2πB.3πC.6πD.6π例16.(2022•永安市校级期中)在三棱锥P-ABC中，PA=BC=4，PB=AC=5，PC=AB=11，则三棱锥P-ABC的外接球的表面积为( )A.26πB.12πC.8πD.24π例17.(2022•罗湖区月考)已知在四面体ABCD中，AB=CD=22,AD=AC=BC=BD=5，则四面体ABCD的外接球表面积为 ．例18.(2022•三模拟)在四面体ABCD中，AC=BD=2，AD=BC=5，AB=CD=7，则其外接球的表面积为 ．题型四:直棱柱模型例19.(2022·山西·太原五中高一阶段练习)在直三棱柱ABC-A1B1C1中，若AB⊥BC,AB=6,BC=8,AA1=6，则该直三棱柱外接球的表面积为(       )A.72πB.114πC.136πD.144π例20.(2022·安徽·合肥市第六中学高一期中)设直三棱柱ABC-A1B1C1的所有顶点都在一个球面上，AB=AC=AA1，∠BAC=120°，且底面△ABC的面积为23，则此直三棱柱外接球的表面积是(       )4010πA.16πB.3C.40πD.64π例21.(2022·河南·高三阶段练习(文))已知正六棱柱ABCDEF-A1B1C1D1E1F1的每个顶点都在球O的球面上，且AB=3，AA1=4，则球O的表面积为(       )A.42πB.48πC.50πD.52π例22.(2022·全国·高二课时练习)表面积为81π的球，其内接正四棱柱(底面是正方形的直棱柱)的高是7，则这个正四棱柱的底面边长为______．例23.(2022·河南·高三阶段练习(