衡阳县一中2025届高三上学期第一次模拟考试卷数学注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。4.考试结束后,请将本试题卷和答题卡一并上交。第Ⅰ卷(选择题)一、单选题(本题共8小题,每小题5分,共40分)1.已知集合A=x1≤x≤3,B=xy=ln2−x,则∁RB∩A=( )A.1,2 B.1,2C.2,3 D.2,32.已知z=21−i1+i,z是z的共轭复数,则z=( )A.0 B.2i C.2 D.−23.“a=3”是“直线y=x+4与圆x−a2+y−32=8相切”的 ( )A.充分不必要条件 B.必要不充分条件C.充要条件 D.既不充分也不必要条件4.如图所示,在边长为3的等边三角形ABC中,AD=23AC,且点P在以AD的中点O为圆心,OA为半径的半圆上,若BP=xBA+yBC,则下列说法错误的是( )A.BD=13BA+23BC B.BD→⋅BO→=132C.BP⋅BC存在最大值为9 D.x+y的最大值为1+395.已知点P为椭圆C:x216+y212=1上任意一点,直线l过⊙M:x2+y2−4x+3=0的圆心且与⊙M交于A,B两点,则PA⋅PB的取值范围是( )A.3,35 B.2,34 C.2,36 D.4,366.有一袋子中装有大小、质地相同的白球k个,黑球2024−kk∈N*.甲、乙两人约定一种游戏规则如下:第一局中两人轮流摸球,摸后放回,先摸到白球者本局获胜但从第二局起,上一局的负者先摸球.若第一局中甲先摸球,记第n局甲获胜的概率为pn,则关于以下两个命题判断正确的是( )①p1=20244048−k,且pn+1=1−2p1pn+p1;②若第七局甲获胜的概率不小于0.9,则k不小于1992.A.①②都是真命题 B.①是真命题,②是假命题C.①是假命题,②是真命题 D.①②都是假命题7.在《九章算术》中,将四个面都为直角三角形的三棱锥称之为鳖臑.如图所示,某同学利用两个完全一样的半圆柱,得到了一个三棱锥A−BCD,该三棱锥为鳖臑,O1,O2为半圆柱的圆心,半径为2,BD=4,∠AO2C=60∘,动点Q在△ACD内运动(含边界),且满足BQ=10,则点Q的轨迹长度为( )A.2π B.3π C.22π D.23π8.已知函数f(x)=e2x+a−12ln(x+5)+a2−5有零点,那么实数a的最大值为( )A.12 B.1 C.1+ln2 D.9−ln2二、多选题(本题共3小题,每小题6分,共18分)9.抛物线C:y2=4x的准线为l,过焦点F的直线与C交于A,B两点,分别过A,B作l的垂线,垂足分别为A',B',记△AA'F,△A'B'F,△BB'F的面积分别为S1,S2,S3,则( )A.△A'B'F为锐角三角形 B.S2的最小值为4C.S1,12S2,S3成等差数列 D.S1,12S2,S3成等比数列10.如图,在三棱锥A−BCD中,AB、BD、BC两两垂直,E为AC上一点,DE⊥AC,M、N分别在直线AB、DE上,AB=2BC=2BD=2,则:( ).A.AC⊥BEB.DE=35C.若平面α//AD且A、B、C、D到α距离相等,则直线DE与α的夹角正弦值为815D.MN的最小值为4414111.在平面直角坐标系xOy中有一点A,A到定点1,1与y轴距离之积为一常数a,A点构成的集合为曲线C,已知C在x>0或x<0分别为连续不断的曲线,则下列说法正确的是:( ). A.曲线C关于直线y=−1对称B.若a=2,则x>0时A到y轴距离的最大值为2C.若x>0,C如图,则a=14D.若C与x轴正半轴交于1,0,则与x轴负半轴的交点横坐标在区间−1,0内第Ⅱ卷(非选择题)三、填空题(本题共3小题,每小题5分,共15分)12.已知函数fx=314x−1+log39+x2+x.若不等式ff−4x+m⋅2x+f−32<0对任意x∈R恒成立,则m的取值范围是.13.已知数列an的前n项和为Sn,满足2Sn=3an−1(n∈N,n≥1),函数fx定义域为R,对任意x∈R都有fx+1=1+fx1−fx,若f2=1−2,则f(a2025)的值为.14.已知F1,F2分别为双曲线x2a2−y2b2=1(a>0,b>0)的左、右焦点,过F2的直线l与双曲线的右支交于A、B两点(其中A在第一象限),△AF1F2的内切圆半径为r1,△BF1F2的内切圆半径为r2,若r1=2r2,则直线l的斜率为.四、解答题(本题共5小题,共77分)15.(13分)已知数列an,其前n项和为Sn,对任意正整数n,Sn=2an−μ恒成立,且a1+a2=12.(1)证明:数列an为等比数列,并求实数μ的值;(2)若bn=1log2an,数列bn前n项和为Tn,求证:Tn>lnn+22;(3)当n≥1时,设集合Bn=ai+aj∣3⋅2n+1
湖南省衡阳市衡阳县第一中学2025届高三上学期第一次模拟考试数学试卷(含答案)
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
湖南省衡阳市衡阳县第一中学2028届高三上学期第一次模拟考试语文试题(含答案)
2024-12-14 17:29
 20页
20页 -
湖南省衡阳县第一中学2025届高三上学期第一次模拟英语试题
2024-12-14 17:29
 25页
25页 -
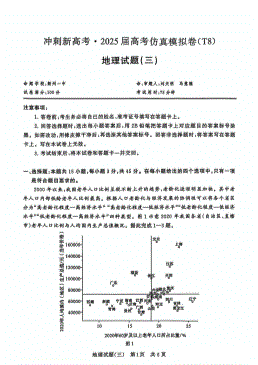
T8冲刺新高考2025届高三仿真模拟卷(三)地理试题及答案
2024-12-14 17:49
 9页
9页 -
T8冲刺新高考2025届高三仿真模拟卷(三)化学试题及答案
2024-12-14 17:49
 13页
13页 -
T8冲刺新高考2025届高三仿真模拟卷(三)语文试题及答案
2024-12-14 17:49
 19页
19页 -
T8冲刺新高考2025届高三仿真模拟卷(三)生物试题及答案
2024-12-14 17:49
 14页
14页 -
T8冲刺新高考2025届高三仿真模拟卷(三)政治试题及答案
2024-12-14 17:49
 13页
13页 -
东三省2024-2025学年高三 上学期12月调研测试数学试题
2024-12-14 17:49
 2页
2页













