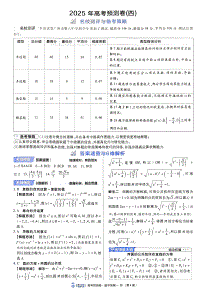
巴中市普通高中2022级“一诊”数学试题参考答案一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的四个选项中，只有一项是符合题目要求的.题号12345678答案BCDACBBD8解析：令f(x)-2=t，则有f(t)=2,f(x)=2+t.由题意得，当t≤0时，方程t2+2t+2=2-22有两根t1=-2,t2=0；当t>0时，方程|lnt|=2有两根t3=e,t4=e.当t1=-2时，f(x)=2+t1=0，则y=f(x)的图像与直线y=0只有一个交点；当t2=0时，f(x)=2+t2=2，则y=f(x)的图像与直线y=2有四个交点；-2-2-2当t3=e时，f(x)=2+t3=2+e，则y=f(x)的图像与直线y=2+e有三个交点；222当t4=e时，f(x)=2+t4=2+e，则y=f(x)的图像与直线y=2+e有三个交点.综上可知：方程f(f(x)-2)=2实数根的个数为11个.故选：D二、多选题：本题共3小题，每小题6分，共18分。在每小题给出的四个选项中，有多项符合题目要求。全部选对的得6分，部分选对的得部分分，有选错的得0分.题号91011答案CDBDABD211111解析：由y=2x得p=,F0,，设直线l：y=kx+，A(x,y),B(x,y),y>0,y>0488112212ppy1+y1+x122|AF|，设AF的中点为M,即M,到x轴的距离d==，则以AF为直径2222的圆与x轴相切，则A正确；1y=kx+22k1联立8，得16x-8kx-1=0，Δ=64k+64>0，x1+x2=,x1x2=-，则y1+y=2x22162k2+11ppy=,yy=，因为|AF|=y+,|BF|=y+2412641222111122+=+=+=8,则B正确；|AF||BF|pp2y1+P2y2+Py+y+1222因为直线过焦点F，设直线AB：mx+8y=1，联立y=2x2(齐次化方程)，得8y2+mxy-2x2y2y=0，两边同除以x2得，8+m-2=0(∗)，则由题意知k,k是(∗)方程得两不等根xx12y1y21k1=,k2=，所以k1k2=-，则C错误；x1x2422由y=2x得y=4x，kAP=4x1，切线AP方程：y-y1=4x1(x-x1)=4x1x-4x1=4x1x-1①2y，即y+y=4xx①，同理切线BP方程：y+y=4xx②，由①-②得，x=k；11122p4AB②·第1页·(共6页)11kx1+x2-kx2+x1y1x2-y2x18811得，yp===-，即点P在y=-上，则D正确.x1-x2x1-x288故选：ABD三、填空题：本题共3小题，每小题5分，共15分.412.13.114.(3,2)514解析：延长F2M交PF1于点Q，连接OM，由题意知|PQ|=|PF2|，又由双曲线的定义得|QF1|=2a，在三角形QF1F2中，点O,M分别为F1F2，QF2的中点，则|OM|=a.a2+c2-3b2c2-2a2设∠MOF=θ，在三角形OMF中，-cosθ=,则cosθ=,因为θ小于渐212acacaac2-2a2近线的倾斜角,所以＜cosθ＜1，即＜＜1解得：3=cos,=cos,=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯14分26m⋅n62t+22BF1解得：t=1，即=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯15分BC218.(17分)解析：(1)f'(x)=lnx+1(x>0)，令f'(x)=0得x=e-1,⋯⋯⋯⋯⋯⋯⋯1分当0e-1时，f'(x)>0，f(x)单调递增；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯2分-1-1f(x)极小值=f(e)=-e,无极大值.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分(2)原不等式等价于：00，所以h(x)在0,e上总有唯一的零点；⋯⋯⋯⋯⋯10分-12②当x>e时，h(x)=x-2t1+lnx，22t2x+tx-t则h'(x)=x-2t1+lnx=2x-=⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11分xx-2-1-1(I)若00在e,+∞上恒成立，h(x)在e,+∞上单调递增，-1-2-1h(x)>h(e)=e>0，h(x)在e,+∞上无零点；⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯12分·第4页·(共6页)(II)若e-2t时，h'(x)>0，h(x)单调递增；-1h(x)min=ht=-t1+lnt，令h(x)min=ht=0，得t=e⋯⋯⋯⋯⋯⋯⋯⋯⋯13分-2-1-1(i)若e0，h(x)在e,+∞上无零点⋯⋯⋯⋯⋯⋯14分-1-1(ii)若t=e，则h(x)min=ht=0，h(x)在e,+∞上有唯一零点⋯⋯⋯⋯⋯⋯15分-1-1-2(iii)若e0，22又由(2)知lnx≤x-1，xlnx≤x-x得，得h2t=4t-2t-2tln2t≥0，-1由零点存在性定理可知，h(x)在e,t，(t,2t]上各有一个零点.⋯⋯⋯⋯⋯⋯16分综上所述：当0