2023届高三湖北十一校第二次联考数学试题参考答案一:选择题123456789101112DDCCCDBBACBCABDAB二:填空题113.448.14.(25,25)15.516.,12三:解答题17.解:若选①,2则(1)由a1a2a3…ann,所以,…2,…………………1分n 2a1a2a3an1(n1)两式相减可得:,22,…………………3分n 2ann(n1)2n1而在…2中令可得:,符合上式,a1a2a3annn1a11故an2n1.…………………5分11111(2)由(1)知:(),…………7分anan1(2n1)(2n1)22n12n1111111所以T[(1)()()]n23352n12n111n(1).……………10分22n12n1若选②则由*可得:数列为等差数列,又因为,(1)2anan1an1(nN,n 2){an}a11,所以,即,所以……………5分a47a4a13dd2an1(n1)22n1.(2)同上.aa若选③,则(1)由点A(n,a),B(n1,a)在斜率是2的直线上得:n1n2,即nn1(n1)n,所以数列为等差数列且………………5分an1an2{an}an1(n1)22n1.(2)同上.1bcosC3bsinC18.解:(1)因为1,所以bcosC3bsinCac0,ac所以sinBcosC3sinBsinCsinAsinC0,…………………1分因为ABC,所以sinBcosC3sinBsinCsinBCsinC0,所以3sinBsinCcosBsinCsinC0,…………………2分1因为C0,,所以sinC0,所以sinB,…………………4分62因为B0,,所以B,66b所以B外接圆半径2R2.所以R=1…………………6分3sinB(2)因为BABC6,有由题可知B,所以ac12,…………………7分3又因为b2a2c22accosB,ac43可得b23,…………………9分1因为SacsinB33.211由ABC的面积SabcracsinB,得r1。…………………12分2219.()过A作ADPB于D,平面PAB平面PBCAD平面PBC,又BC平面PBC1.ADBC…………………2分又PA平面ABCE,BC平面ABCEPABC…………………4分BC平面PAD,又AB平面PADBCAB…………………5分)以B为坐标原点,BA,BC为x,y轴,过B平行于PA的(直2线.为Z轴建立空间直角坐标系,B(0,0,0),A(0,1,0),C(0,2,0)P(1,0,22)又设E(x,y,0),BE22,x2y28①ACAE,(x1)2y25②2由①②得x2,y2,E(2,2,0)…………………7分422222又P(1,0,22),故G(1,,),CG(1,,)…………………8分3333设平面PBC的法向量为n(x,y,z)n,BP0x220则令,…………………10分n,BC02y0x1n(22,0,1)设CG与平面所成的角为.CGn442则sin.…………………12分CGn631b20.解:(1)令u,则ya可转化为yabu,xx8uy8uy184ii93.0680.3423因为,所以ˆi1,y23b82508221.5380.34ui8ui150所以aˆybu6,所以y650u,所以y关于x的回归方程为y6;……4分x(2)因为,所以用反比例函数模型拟合效果更好,|r1||r2|把x10代入回归方程得y11(元),所以产量为10千件时每件产品的非原料成本约为11元;……………………7分184(3)因为y23,所以23,88因为样本标准差为1221,s(yi8y)(5777.5582323)193.19413.98i18所以13.9,所以非原料成本y服从正态分布N(23,13.92),…………………9分所以(,)(2313.9,2313.9)(9.1,36.9),因56.5在(,)之外,所以需要此非原料成本数据寻找出现异样成本的原因.…12分21.(1):设直线的方程为BCxmyn,B(x1,y1),C(x2,y2)将A(2,2)代入抛物线方程得p1…………1分30xmyn2联立2y2my2n0y1y22my2xy1y22n…………2分BOC90OBOCx1x2y1y20(my1n)(my2n)y1y2022(m1)y1y2mn(y1y2)n02m2n2n2m2nn20n22n0n0或n2…………………5分若n0,直线BC的方程为xmy,恒过定点(0,0),不合题意舍;若n2,直线BC的方程为xmy2,恒过定点(2,0).………………………6分1(2)解析:方法1:设直线BC的方程为xmy,B(x,y),C(x,y)2112210xmy22y2my10y1y22m2y2xy1y21yyyy2myy(yy)kk12121212BFCF11my1my1(my1)(my1)xx12121222……………8分2m2m0(my11)(my21)不妨设直线BF的倾斜角为(0),22tan24444则tan2tan,k,k1tan273BF3CF3yy2y4111111kBF22y1B(,)1y11y113282x12224kkA,F,B共线………………………10分AF3BF12SAFACF24.………………………12分11SBCFBF821方法2:设直线BC的方程为xmy,B(x,y),C(x,y)21122410xmy22y2my10y1y22m2y2xy1y2111117FA(x,y),FB(x,y),BFx,CFx,cosBFC12122212222511(x)(x)yyFAFB1212(my1)(my1)yycosFA,FB22121211(my)(my)FBFB(x)(x)121222(m21)yym(yy)1m212m212m2751212……8分222mmy1y2mm2545由于直线BC过点Q,B,C在x轴下方,m…………9分4111代入y22my10得y,y2B(,)…………10分122824kkA,F,B共线AF3BF12SAFACF24………………………12分11SBCFBF82其它方法:①利用面积相等建立等量关系求m;②利用余弦定理建立等量关系求m;1lnx22.解析:(1)因为f(x)有2个零点,所以方程有2个根.…………………1分nnxlnx1lnx令g(x),则g(x),xx2所以g(x)在(0,e)上单调递增,在(e,)上单调递减.1因此g(x)在x=e处取得最大值g(e)…………………2分e11所以,即有ne,且有xey(nN*)………………3分nenn1lnxn1lnxn1又,,结合函数g(x)单调性可得,xn1xn,yn1yn,nxnn1xn1所以ynxnyn1xn1………………………5分(2)由fn()fn()fn()()得f()f()n(lnln)n(lnln)f()nn1.n2n而f()1,所以n25n(lnln)2nn2()f()f()[ln].……………7分nn22()2(t1)设t(t1),则lnlnt.………………8分t12(t1)12[(t1)(t1)](t1)2令g(t)lnt(t1),则g(t)0………9分t1t(t1)2t(t1)2所以g(t)在(1,)上单调递增,因此g(t)>g(1)=0.2()故ln0………………………10分n又0,ne,即-0,所以0,从而f()f()0,-nn2n又因为f(x)1在(0,)上递增,所以,得证…………………12分nx26
2023届高三十一校第二次联考 数学答案
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
2023届高三十一校第二次联考 英语答案
2023-11-22 21:28
 6页
6页 -
2023届高三十一校第二次联考 地理答案
2023-11-22 21:28
 4页
4页 -
2023届高三十一校第二次联考 语文答案
2023-11-22 21:28
 4页
4页 -
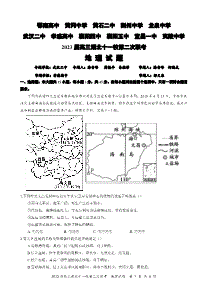
2023届高三十一校第二次联考 地理
2023-11-22 21:28
 6页
6页 -
2023届高三十一校第二次联考 历史答案
2023-11-22 21:28
 4页
4页 -
2023届高三十一校第二次联考 历史
2023-11-22 21:28
 6页
6页 -
2023届高三十一校第二次联考 生物学
2023-11-22 21:28
 4页
4页 -
2023届高三十一校第二次联考 思想政治
2023-11-22 21:28
 3页
3页













