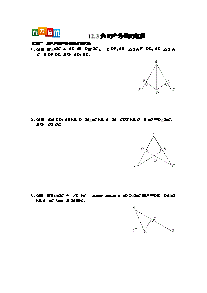
11.2与三角形有关的角专题一利用三角形的内角和求角度1．如图，在△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于D点，∠A=50°，则∠D=（ ）A．15°B．20°C．25°D．30°2．如图，已知：在直角△ABC中，∠C=90°，BD平分∠ABC且交AC于D.若AP平分∠BAC且交BD于P，求∠BPA的度数．3．已知：如图1，线段AB、CD相交于点O，连接AD、CB，如图2，在图1的条件下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB分别相交于M、N．试解答下列问题：（1）在图1中，请直接写出∠A、∠B、∠C、∠D之间的数量关系：__________；（2）在图2中，若∠D=40°，∠B=30°，试求∠P的度数；（写出解答过程）（3）如果图2中∠D和∠B为任意角，其他条件不变，试写出∠P与∠D、∠B之间的数量关系．（直接写出结论即可）[来源专题二利用三角形外角的性质解决问题4．如图，∠ABD，∠ACD的角平分线交于点P，若∠A=50°，∠D=10°，则∠P的度数为（ ） A．15° B．20° C．25° D．30°5．如图，△ABC中，CD是∠ACB的角平分线，CE是AB边上的高，若∠A=40°，∠B=72°．（1）求∠DCE的度数；（2）试写出∠DCE与∠A、∠B的之间的关系式．（不必证明）6．如图：（1）求证：∠BDC=∠A+∠B+∠C；（2）如果点D与点A分别在线段BC的两侧，猜想∠BDC、∠A、∠ABD、∠ACD这4个角之间有怎样的关系，并证明你的结论．状元笔记【知识要点】1．三角形内角和定理三角形三个内角的和等于180°．2．直角三角形的性质及判定性质：直角三角形的两个锐角互余．判定：有两个角互余的三角形是直角三角形．3．三角形的外角及性质外角：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．性质：三角形的外角等于与它不相邻的两个内角的和．【温馨提示】1．三角形的外角是一边与另一边的延长线组成的角，而不是两边延长线组成的角．2．三角形的外角的性质中的内角一定是与外角不相邻的内角．【方法技巧】1．在直角三角形中已知一个锐角求另一个锐角时，可直接使用“直角三角形的两个锐角互余”．2．由三角形的外角的性质可得出：三角形的外角大于任何一个与它不相邻的内角．参考答案:1．C解析：∵∠ABC的平分线与∠ACB的外角平分线相交于点D，∴∠1=∠ACE，∠2=∠ABC．又∵∠D=∠1－∠2，∠A=∠ACE－∠ABC，∴∠D=∠A=25°．故选C．2．解：（法1）因为∠C=90°，所以∠BAC＋∠ABC=90°，所以(∠BAC＋∠ABC)=45°.因为BD平分∠ABC，AP平分∠BAC，∠BAP=∠BAC，∠ABP=∠ABC，即∠BAP＋∠ABP=45°，所以∠APB=180°－45°=135°.[来源:www.shulihua.net数理化网]（法2）因为∠C=90°，所以∠BAC＋∠ABC=90°，所以(∠BAC＋∠ABC)=45°，[来源:学§科§网]因为BD平分∠ABC，AP平分∠BAC，∠DBC=∠ABC，∠PAC=∠BAC，所以∠DBC＋∠PAD=45°.[来源:www.shulihua.net]所以∠APB=∠PDA＋∠PAD=∠DBC＋∠C＋∠PAD=∠DBC＋∠PAD＋∠C=45°＋90°=135°.3．解：（1）∠A+∠D=∠B+∠C；（2）由（1）得，∠1+∠D=∠3+∠P，∠2+∠P=∠4+∠B，∴∠1－∠3=∠P－∠D，∠2－∠4=∠B－∠P，又∵AP、CP分别平分∠DAB和∠BCD，∴∠1=∠2，∠3=∠4，∴∠P－∠D=∠B－∠P，即2∠P=∠B+∠D，∴∠P=（40°+30°）÷2=35°．（3）2∠P=∠B+∠D．4．B解析：延长DC，与AB交于点E．根据三角形的外角等于不相邻的两内角和，可得∠ACD=50°+∠AEC=50°+∠ABD+10°，整理得∠ACD－∠ABD=60°．设AC与BP相交于点O，则∠AOB=∠POC，∴∠P+∠ACD=∠A+∠ABD，即∠P=50°－（∠ACD－∠ABD）=20°．故选B．5．解：（1）∵∠A=40°，∠B=72°，∴∠ACB=68°．∵CD平分∠ACB，∴∠DCB=∠ACB=34°．∵CE是AB边上的高，∴∠ECB=90°－∠B=90°－72°=18°．∴∠DCE=34°－18°=16°．（2）∠DCE=（∠B－∠A）．6．（1）证明：延长BD交AC于点E，∵∠BEC是△ABE的外角，∴∠BEC=∠A+∠B．∵∠BDC是△CED的外角，∴∠BDC=∠C+∠DEC=∠C+∠A+∠B．（2）猜想：∠BDC+∠ACD+∠A+∠ABD=360°．证明：∠BDC+∠ACD+∠A+∠ABD=∠3+∠2+∠6+∠5+∠4+∠1=（∠3+∠2+∠1）+（∠6+∠5+∠4）=180°+180°=360°．