2024届高三二轮复习“8+4+4”小题强化训练(7)一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合,则()A. B. C. D.【答案】C【解析】或,,则,故选:C.2.如图,在复平面内,复数,对应的点分别为,,则复数的虚部为()A. B. C. D.【答案】D【解析】在复平面内,复数,对应的点分别为,,则,,得,所以复数的虚部为.故选:D3.若古典概型的样本空间,事件,甲:事件,乙:事件相互独立,则甲是乙的()A.充分不必要条件 B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件【答案】A【解析】若,,则,而,,所以,所以事件相互独立,反过来,当,,此时,,满足,事件相互独立,所以不一定,所以甲是乙的充分不必要条件.故选:A4.在平行四边形中,.若,则()A. B. C. D.【答案】D【解析】,所以,则.故选:D5.已知为双曲线的左焦点,直线与交于两点,且轴,则的离心率为()A. B. C. D.【答案】C【解析】易知直线经过的左顶点,设,因为轴,所以,解得,或(舍去),所以点坐标为,则,整理得,所以,即,解得(舍去),或,所以的离心率为,故C正确.故选:C.6.定义在上的函数和的图象关于轴对称,且函数是奇函数,则函数图象的对称中心为()A. B. C. D.【答案】C【解析】由函数为奇函数,可得,令,可得,所以函数的图象关于点对称,又因为与的图象关于轴对称,所以函数图象的对称中心为.故选:C.7.如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中,后人称为“三角垛”.“三角垛”的最上层有1个球,第二层有3个球,第三层有6个球,第四层有10个球…….记第层球的个数为,则数列的前20项和为()A. B. C. D.【答案】C【解析】根据已知条件有,当时,,,,,,以上各式累加得:,又,所以,经验证符合上式,所以;所以,设数列的前项和为,则,所以.故选:C8.如图,水利灌溉工具筒车的转轮中心到水面的距离为,筒车的半径是,盛水筒的初始位置为与水平正方向的夹角为.若筒车以角速度沿逆时针方向转动,为筒车转动后盛水筒第一次到达入水点所需的时间(单位:),则() B. C. D.【答案】C【解析】设盛水桶在转动中到水面的距离为,时间为,由题意可得,盛水桶到水面的距离与时间的函数关系如下:,令,即,解得,又,可得,,,故C正确;,,,故D错误;又,解得,故B错误;,解得,故A错误.故选:C.二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知复数(为虚数单位),则下列说法中正确的是()A.的共轭复数是 B.C.的辐角主值是 D.【答案】BCD【解析】因为,所以,故A错误;,故B正确;,故C正确;,故D正确.故选:BCD10.已知函数,则()A.函数为偶函数B.曲线对称轴为C.在区间单调递增D.的最小值为【答案】AC【解析】,即,对于A,,易知为偶函数,所以A正确;对于B,对称轴为,故B错误;对于C,,单调递减,则单调递增,故C正确;对于D,,则,所以,故D错误;故选:AC11.四棱锥的底面为正方形,与底面垂直,,,动点在线段上,则()A.不存在点,使得 B.的最小值为C.四棱锥的外接球表面积为 D.点到直线的距离的最小值为【答案】BD【解析】对于A:连接,且,如图所示,当在中点时,因为点为的中点,所以,因为平面,所以平面,又因为平面,所以,因为为正方形,所以.又因为,且,平面,所以平面,因为平面,所以,所以A错误;对于B:将和所在的平面沿着展开在一个平面上,如图所示,则的最小值为,直角斜边上高为,即,直角斜边上高也为,所以的最小值为,所以B正确;对于C:易知四棱锥的外接球直径为,半径,表面积,所以C错误;对于D:点到直线距离的最小值即为异面直线与的距离,因为,且平面,平面,所以平面,所以直线到平面的距离等于点到平面的距离,过点作,因为平面,所以,又,且,故平面,平面,所以,因为,且,平面,所以平面,所以点到平面的距离,即为的长,如图所示,在中,,,可得,所以由等面积得,即直线到平面的距离等于,所以D正确,故选:BCD.12.已知圆,直线l过点,若将圆C向上平移4个单位长度,再向右平移3个单位长度得到圆,则下列说法正确的有()A.若直线l与圆C相切,则直线l的方程为B.若直线l与圆C交于A,B两点,且的面积为2,则直线l的方程为或C.若过点的直线与圆C交于M,N两点,则当面积最大时,直线的斜率为1或D.若Q是x轴上的动点,,分别切圆于R,S两点,则直线RS恒过定点【答案】BCD【解析】对于A选项:当直线l垂直于x轴时,其方程为,符合题意.当直线l不垂直于x轴时,设直线l的方程为,即,则,解得,所以直线l的方程为,即.综上,直线l的方程为或,所以A错误;对于B选项:由题意知直线l斜率存在且不为0,故设直线l的方程为,即.设圆心C到直线l的距离为,则,即,解得,则,解得或.所以直线l的方程为或,所以B正确;对于C选项:可知直线的斜率存在且不为0,设直线的方程为,即,所以圆心到直线的距离.因为,当且仅当,即时取等号.由,得,解得或,所以C正确;对于D选项:由题意知圆的方程为,圆心.设,则以为直径的圆的圆心为,半径为,则圆D的方程为,整理得,圆与圆D的公共弦所在直线即为直线RS,将两式相减,可得直线RS的方程为,即.令解得即直线RS恒过定点,所以D正确.故选:BCD.三、填空题:本题共4小题,每小题5分,共20分.13.已知指数函数的图象经过点,则__________.【答案】4【解析】由题意设,且,图象经过点,则,解得,所以,.故答案为:4.14.与圆台的上、下底面及侧面都相切的球,称为圆台的内切球,若圆台的上下底面半径为,,且,则它的内切球的体积为______.【答案】【解析】由题意,画出圆台的直观图,其中为圆台的母线长,,分别为上、下底面的圆心,点为内切球的球心,点为球与圆台侧面相切的一个切点.则由题意可得:,.因此可得:内切球半径,即得内切球的体积为.故答案为:15.甲和乙两个箱子中各装有10个除颜色外完全相同的球,其中甲箱中有4个红球、3个白球和3个黑球,乙箱中有5个红球、2个白球和3个黑球.先从甲箱中随机取出一球放入乙箱,分别用、和表示由甲箱取出的球是红球、白球和黑球的事件;再从乙箱中随机取出一球,用B表示由乙箱取出的球是红球的事件,则__________【答案】【解析】由题意得,,,若发生,此时乙箱中有6个红球,2个白球和3个黑球,则,先发生,此时乙箱中有5个红球,3个白球和3个黑球,则,先发生,此时乙箱中有5个红球,2个白球和4个黑球,则.,;.故答案为:16.已知为拋物线的焦点,过点的直线与拋物线交于不同的两点,,拋物线在点处的切线分别为和,若和交于点,则的最小值为__________.【答案】10【解析】的焦点为,设直线方程为,.联立直线与抛物线方程有,则.又求导可得,故直线方程为.又,故,同理.联立可得,解得,代入可得,代入韦达定理可得,故.故,当且仅当,即时取等号.故答案为:10
“8+4+4”小题强化训练(7)-2024届高三数学二轮复习《8+4+4》小题强化训练(新高考地区专
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
“8+4+4”小题强化训练(4)-2024届高三数学二轮复习《8+4+4》小题强化训练(新高考地区专
2024-01-27 22:08
 3页
3页 -
“8+4+4”小题强化训练(4)-2024届高三数学二轮复习《8+4+4》小题强化训练(新高考地区专
2024-01-27 22:08
 10页
10页 -
内蒙古包头市2023-2024学年高三上学期期末考试理科综合化学答案
2024-01-27 22:10
 3页
3页 -
内蒙古包头市2023-2024学年高三上学期期末考试理科综合生物答案
2024-01-27 22:10
 2页
2页 -
内蒙古包头市2023-2024学年高三上学期期末考试理科综合物理答案
2024-01-27 22:10
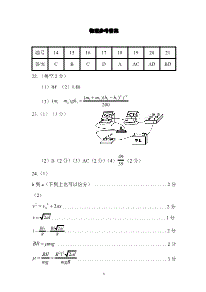 4页
4页 -
内蒙古包头市2023-2024学年高三上学期期末考试语文答案
2024-01-27 22:10
 2页
2页 -
内蒙古包头市2023-2024学年高三上学期期末教学质量检测文科数学试题
2024-01-27 22:10
 2页
2页 -
内蒙古包头市2023-2024学年高三上学期期末考试文科数学答案
2024-01-27 22:10
 3页
3页













