吴忠市2024届高考模拟联考试卷(一)理数参考答案一、选择题(每小题5分,共60分)题号123456789101112答案ABADCBDBACBD二、填空题(每小题5分,共20分)13.-214.15.16.18155160三、解答题(共70分)217.解:(1)该校男生支持方案一的概率为,……………………3分????��????�+????�=�该校女生支持方案一的概率为;……………………6分????��????�+????�=�(2)3人中恰有2人支持方案一分两种情况,(1)仅有两个男生支持方案一,(2)仅有一个男生支持方案一,一个女生支持方案一,……………………8分所以3人中恰有2人支持方案一概率为:;………………………12分���������(�)(�−�)+��(�)(�−�)�=????18.解:(1)由已知得∠PBC=60°,所以∠PBA=30°.……………………2分117在△PBA中,由余弦定理得PA2=323cos30.…………5分4247故PA=.……………………6分2(2)设∠PBA=α,由已知得PB=.……………………8分sinα3sin在△PBA中,由正弦定理得,………………10分sin150sin(30)化简得3cosα=4sinα.……………………11分33所以=,即tan∠PBA=……………………12分44????????理数答案·第1页·共5页{#{QQABDYQAggAgAJBAAQgCEQVQCkIQkBCCCCoOgEAIsAAAiBNABAA=}#}19.解:(1)证明:因为四边形CDEF为正方形,所以EDDC,又平面CDEF平面ABCD,平面CDEF平面ABCDDC,DE平面CDEF,所以ED平面ABCD.因为BD平面ABCD,所以BDED.……………………2分在△ABD中,因为ADC120,故DAB60,不妨设AB2AD2,所以由余弦定理,得BD2AB2AD22ABADcos603,则BD3,所以AD2BD2AB2,所以ADBD,……………………4分又EDADD,ED,AD平面ADE,所以BD平面ADE.……………………6分(2)解:过点D作DMAB交AB于点M,则DMDC,平面CDEF平面ABCD,平面CDEF平面ABCDDC,DM平面ABCD,所以DM平面CDEF.……………………7分31如图建立空间直角坐标系,则D0,0,0,F0,1,1,A,,0,2233E0,0,1,B,,0,223133所以AE,,1,DF0,1,1,DB,,0,………8分2222设平面BDF的法向量为nx,y,z,nDFyz0则,33nDBxy022令y1,则z1,x3,所以n3,1,1,………10分设直线AE与平面BDF所成角为,理数答案·第2页·共5页{#{QQABDYQAggAgAJBAAQgCEQVQCkIQkBCCCCoOgEAIsAAAiBNABAA=}#}313111所以AEn2210,sinAEn521010所以直线AE与平面BDF所成角的正弦值为;……………12分1020.解:(1)由已知,设椭圆的方程为22………………2分���22�+�=1,�>0且经过点(,),则t=2,12故椭圆的标准方程为22;……………………5分���24+2=1(2)依据题意,直线AP,AQ的斜率存在且不为0,A(0,2),设直线AP的斜率为,直线AQ的斜率为,12设P,则Q��(x0,y0)(−x0,−y0)因为22所以,�0�0224+2=1,�0−4=−2�0所以,�0−2−�0−2�1�2=�0×−�0=−2即=,……………………7分12直线��AP:−2与8,联立得2222y=k1x+2x+2y=(1+2k1)x+8k1x=0解得,同理可得,……………………8分−8�1−8�2�2�2�=1+2k1�=1+2k2直线AP:与4,联立得,2222y=k1x+22x+y=(2+k1)x+4k1x=0接的,同理可得……………………9分−4�1−4�2�2�2�=2+k1�=2+k222�1|��||��|����|64�1�2|(2+k1)(2+k2)22�2=|��||��|=|��|×|��|=(1+2k1)(1+2k2)×|16�1�2|=22224(4+2�1+2�2+4)32+8(�1+�2)22222�1+2�2+17=17+2(�1+�2),因为………………11分362224221212=4−17+2(�1+�2)�+�=�+�1≥4.当且仅当,即时,等号成立,24121�=�1�=±2故的取值范围为…………12分�164�2[25,4)理数答案·第3页·共5页{#{QQABDYQAggAgAJBAAQgCEQVQCkIQkBCCCCoOgEAIsAAAiBNABAA=}#}21.解:(1)易知函数f(x)的定义域为.由f(x)=0,可得(0,+∞)1�lnx−x+x=0.设,1�(x)=�lnx−x+x则,2,且(x)与f(x)有相同的零'�1−�+��−122�(1)=0�(�)=�−1−�=��点个数.……………………1分令,x>0,则22①当φ(x)=−2时�,+��−,1则∆=,�即−4,可得(x)在'单−2调≤递�减≤,则(∆x≤)0有且仅φ有(x一)≤个0零点.�(�)≤0………�…………(0…,3+分∞)②当时,显�然,则,'可得�<(−x2)在φ(x单)调<递0减,�则(�()
宁夏吴忠市2024届高三下学期高考模拟联考(一)理科数学试卷答案
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
宁夏吴忠市2024届高三下学期高考模拟联考(一)历史试题答案
2024-03-26 17:10
 3页
3页 -
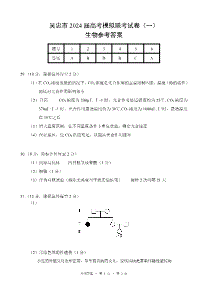
宁夏吴忠市2024届高三下学期高考模拟联考(一)生物试题答案
2024-03-26 17:10
 2页
2页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)理科数学试卷
2024-03-26 17:10
 4页
4页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)文科数学试卷
2024-03-26 17:10
 4页
4页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)文科数学试卷答案
2024-03-26 17:10
 8页
8页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)物理试题答案
2024-03-26 17:10
 3页
3页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)英语试题答案
2024-03-26 17:10
 5页
5页 -
宁夏吴忠市2024届高三下学期高考模拟联考(一)语文试题答案
2024-03-26 17:10
 10页
10页













