函数值域的求法8大题型命题趋势函数的值域是函数概念中三要素之一,是高考中的必考内容,具有较强的综合性,贯穿整个高中数学的始终。在高考试卷中的形式千变万化,但万变不离其宗,真正实现了常考常新的考试要求,考生在复习过程中首先要掌握一些简单函数的值域求解的基本方法,其次要多看多练在其他板块中涉及值域类型的内容。满分技巧一、求函数值域的常见方法1.直接法:对于简单函数的值域问题,可通过基本初等函数的图象、性质直接求解;2.逐层法:求f1(f2⋯fn(x))型复合函数的值域,利用一些基本初等函数的值域,从内向外逐层求函数的值域;3.配方法:配方法是二次型函数值域的基本方法,即形如“y=axx+bx+c(a≠0)”或“y=a[f(x)]2+bf(x)+c(a≠0)”的函数均可用配方法求值域;4.换元法:利用换元法将函数转化为易求值域的函数,常用的换元有ax+bcx+d(1)y=或y=的结构,可用“cx+d=t”换元;cx+dax+b(2)y=ax+b±cx+d(a,b,c,d均为常数,a≠0,c≠0),可用“cx+d=t”换元;ππ(3)y=bx±a2-x2型的函数,可用“x=acosθ(θ∈[0,π])”或“x=asinθθ∈-,”换元;22ax+bax+ba5.分离常数法:形如y=(ac≠0)的函数,应用分离常数法求值域,即y==+cx+dcx+dcbc-ad,然后求值域;c2x+dcb6.基本不等式法:形如y=ax+(ab>0)的函数,可用基本不等式法求值域,利用基本不等式法求函x数的值域时,要注意条件“一正、二定、三相等”,即利用a+b≥2ab求函数的值域(或最值)时,应满足三个条件:①a>0,b>0;②a+b(或ab)为定值;③取等号的条件为a=b,三个条件缺一不可;7.函数单调性法:确定函数在定义域上的单调性,根据函数单调性求出函数值域(或最值)(1)形如y=ax+b-cx+d(ac<0)的函数可用函数单调性求值域;b(2)形如y=ax+的函数,当ab>0时,若利用基本不等式等号不能成立时,可考虑利用对勾函数x求解;高考加油b当ab<0时,y=ax+在(-∞,0)和(0,+∞)上为单调函数,可直接利用单调性求解。xasinxacosx8.函数的有界性法:形如y=(或y=)(其中a,b,c不为0)的函数求值域或最值,c+bsinxc+bcosxc可用y表示出sinx(或cosx),再根据-1≤sinx≤1且sinx≠-(或-1≤cosx≤1且cosx≠bc-),列出关于y的取值范围.b类似地,有:①x2=f(y),则f(y)≥0;②ax=h(y),则h(y)>0;③sinx=g(y),则-1≤g(y)≤12a2x+b2x+c229.判别式法:形如y=2(a1a2≠0)或y=Ax+Bax+bx+c(ABa≠0)的函数求值域,a1x+b1x+c1可将函数转化为关于x的方程F(x,y)=0,利用二次项系数不为0,判别式Δ≥0或二次项系数为0,一次方程有解得出函数的值域。10.导数法:对可导函数f(x)求导,令f(x)=0,求出极值点,判断函数单调性;如果定义域是闭区间,则函数最值一定取在极值点处或区间端点处;如果定义域是开区间且函数存在最值,则函数最值一定取在极值点处。二、根据最值条件求解参数范围解题思路已知函数的最值求参数范围时,要视参数为已知数,结合函数值域(或最值)的求法,得到函数的最值(含有参数),再与给出的函数最值作比较,求出参数范围。热点题型解读【题型1单调性法求函数值域或最值】1【例1】(2022秋·陕西西安·高三校考期中)函数f(x)=-2x在区间[1,2]上的最小值是()x77A.-B.C.1D.-122【答案】A1【解析】在区间[1,2]单调递减,-2x在区间[1,2]也单调递减,x17所以fx在区间[1,2]单调递减,因此f(x)=f(2)=-22=-,故选:Amin22【变式1-1】(2022秋·北京·高三北京市第一六一中学校考期中)已知函数fx=ex+x,则fx的值域是_____.【答案】1,+∞【解析】由已知,可得f-x=fx,即函数为偶函数.又x≥0时,y=ex为增函数,y=x为增函数,所以,fx=ex+x为0,+∞上的增函数,则fx≥f1=1所以,fx的值域是1,+∞.π4【变式1-2】(2022春·浙江舟山·高三校考开学考试)已知x∈0,,则函数y=cosx+()2cosxA.有最小值4B.有最大值4C.无最小值D.有最大值+∞【答案】Cπ【解析】x∈0,时,cosx∈(0,1),2π4因为t=cosx在x∈0,上递减,y=t+在t∈(0,1)上单调递减,2t4函数y=cosx+是定义域上的单调增函数,cosx且y>1+4=5,其值域是(5,+∞);所以函数无最大、最小值.故选:C【变式1-3】(2022·全国·高三专题练习)函数f(x)=lnx+ln(2-x)的最大值为______.【答案】0【解析】由f(x)=lnx+ln(2-x)=ln[-(x-1)2+1],且0
高三数学函数值域的常见求法8大题型(解析版)
你可能还喜欢
购买VIP会员享超值特权
VIP专享免费下载,付费文档最高省50%
免费下载
付费折扣
身份标识
文档工具
限时7.4元/月购买VIP
相关推荐
-
函数中的同构问题--2024高考数学压轴大题秒杀(学生版)
2023-11-18 10:47
 13页
13页 -
函数中的同构问题--2024高考数学压轴大题秒杀(解析版)
2023-11-18 10:47
 21页
21页 -
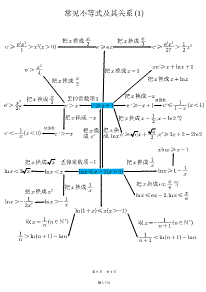
常见不等式放缩关系
2023-11-18 10:48
 2页
2页 -
导数中的隐零点代换与估计问题(解析版)
2023-11-18 10:48
 9页
9页 -
20种排列组合问题的具体方法技巧
2023-11-18 10:48
 7页
7页 -
导数中八大切线问题题型总结(解析)
2023-11-18 10:48
 30页
30页 -
高考数学命题改革分析及复习教学建议(章建跃)
2023-11-18 10:48
 80页
80页 -
构造对偶式的八种途径
2023-11-18 10:48
 8页
8页













