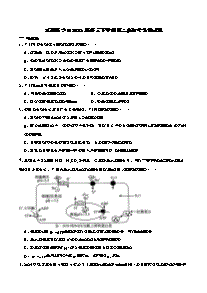
哈尔滨师大附中C.(a2b)−1b=D.(a2b)−1b=−2025年高三第二次联合模拟考试东北师大附中6.已知函数fx()e=|1|xm+−满足fx(1fx)−(=1)−，则（）数学辽宁省实验中学A.fx()fm()B.f(x−1)f(m)注意事项：C.函数fx()x−有1个零点D.函数fx()m−有1个零点1.答卷前，考生务必将自己的姓名、准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如7.已知数列a满足aaaa==+++3,414，则a=（）需要改动，用橡皮擦干净后，再选涂其它答案标号.回答非选择题时，将答案写在答n11nnn+n题卡上，写在本试卷上无效.A.an=+21B.an=2C.an=−412D.an=+413.考试结束后，将本试卷和答题卡一并交回.nnnn第Ⅰ卷（选择题共58分）xxx2−,0,8.已知函数fx()=若xxRxx1212,,,则（）一、单项选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项符合xxxln,0,题目要求.xxfxfx++()()A.f()1212221.已知集合Axx=−{|10}，Bxx={Z|4}2，则AB=（）1B.当xx时，()[()()]0xxfxfx−−1221212A.{2,1,0,1,2}−−B.{2,1,0,2}−−C.{2,1,0}−−D.{−1,0,2}C.当fxfx()()=时，xx+1ii(1)+12122.若z=，则（）1−iD.当fxfxfxfx()()0,()()0−+=−+=时，xx0112212zA.zz+=0B.zz−=0C.zz=−1D.=i二、多项选择题：本大题共3小题，每小题6分，共18分，在每小题给出的四个选项中，有多项符合z题目要求,全部选对的得6分，部分选对的得部分分，有选错的得0分.9.下列说法中正确的是（）3.已知直线xy−+=210与圆(2)(1)xya−++=222相切，则正实数a的值为()A.数据1，2，5，7，8，9，11，15的上四分位数是1035255A.5B.C.D.B.设样本数据xxx12,,,n的方差为5，则2,2,,2xmxmxm12+++n的标准差为20555C.随机掷一枚质地均匀的正方体骰子，骰子各个面分别标记有1～6共六个数字，记事件A＝“骰子4.某同学测得连续7天的最低气温（均为整数）分别为（单位：），若这组数据的平−−6,1,2,t,2,1,5℃向上的点数是奇数”，事件B＝“骰子向上的点数是2或3”，则事件A与事件B是相互独立事件均数与中位数相等，则t=()1D.在二项式()x−n的展开式中,若只有第4项的二项式系数最大，则各项系数和是64A.5B.6C.10D.112x5.已知向量ab,满足a=(1,0),|b|=|2a−b|，则下列结论一定成立的是（）10.已知函数f(x)=−2sinx+cosx,若xf00xf(,−x),()(且)，则下列说法正确的是（）A.(a−2b)a=−1B.(a−2b)a=1A.函数f()x−x0为偶函数B.函数f()x+x0为偶函数数学试卷第1页（共3页）{#{QQABRYAowgg4kBaACI5LA0mkCEgQkJEiLWosRQCeqAwjgBFABAA=}#}四、解答题：本大题共5小题，共77分.解答题应写出文字说明、证明过程或演算步骤.C.fx(f)x()−0D.区间(0,)x0+上fx()单调递减15.（满分13分）已知函数fxaxxaaR()ln()=−+4．11.如图，四棱锥SA−BCD的外接球球心为点O,且底面ABCD为正方形,SA⊥平面ABCD，AB==3,SC23.若点M为SD上靠近点D的三等分点，点PQ,分别为线段SC与平面SAB上的（1）当a=2时，求曲线yf=x()在点(1,(1)f)处的切线方程；点，则PMP+Q最小时，下列说法正确的是（）S（2）若fx()有极大值，且极大值大于0，求实数a的取值范围.A.OMS⊥CB.点P为线段的中点C.平面MPQ截四棱锥所得的截面是直角梯形MAD61D.三棱锥SA−MQ的体积为BC16.（满分15分）已知锐角ABC，角A,B,C所对的边分别为a,b,c，且a=3，3cosB+b=c.32第Ⅱ卷（非选择题共92分）（1）求A；三、填空题：本大题共3小题，每小题5分，共15分.2b2+c253（2）求的取值范围.12.(112++xx)()的展开式中x的系数为_________.（用数字作答）bcxy2213.已知双曲线的左、右焦点分别为，过且斜率为的直线交双22−=10,0(ab)F1,F2F23lab曲线右支于点A（在第一象限），AF12F的内心为I，直线AI交x轴于点P，且|AI|2|=IP|，则双4曲线的离心率为_________.17.（满分15分）如图，四棱锥PABCD−的体积为，底面ABCD为平行四边形，PA⊥底面ABCD，314.图1所示几何体是一个星形正多面体,称为星形十二面体,是由6对(12个)平行五角星面组成的,每对平行五角星面角度关系如图2所示.一个星形十二面体有_________个星芒(凸起的正五棱锥),将所有PBC的面积为2．的星芒沿其底面削去后所得几何体和星形十二面体的表面积之比是_________.（1）求点A到平面PBC的距离；25（2）设APAB=，二面角APBC−−为90，求直线PD与平面PBC所成角的正弦值.(参考数据:tan218=1−)5PAB图1图2DC数学试卷第2页（共3页）{#{QQABRYAowgg4kBaACI5LA0mkCEgQkJEiLWosRQCeqAwjgBFABAA=}#}18.（满分17分）某地区冬季流感频发，为了加强流感疾病的防治，该地区鼓励个人接种流感疫苗，最219.（满分17分）已知抛物线Cy:4x=，焦点为F0.抛物线上有一点Pxyxy11111(,)(1,0)，直线FP01后统计表明，该地区整个冬季的流感患病率是52.28%，至冬季结束仍然有95%的居民未接种疫苗，这与抛物线的另一个交点为P0.按照如下方式依次构造点F21k−，P2k，P21k+，F2k(1k,2=,3,)，过P21k−作些没有接种过流感疫苗的居民的患病率为55%.x轴的垂线，垂足为F21k−，垂线与抛物线C的另一个交点为P2k.作直线PF2kk−−221，与抛物线的另一（1）现从接种过疫苗的人群中任选一位居民，求这人患病的概率；个交点为P21k+，直线PP2kk2+1与x轴的交点为F2k.记Pnxn(ny,)，Fmnn(,0)，mm1=，(n=0,1,2,).k（2）已知泊松分布的概率分布列为PXkek()(0,1,2,)===−，其中e为自然对数的底数，是泊松k!（1）若P1(2,22)，求m0，m1，m2，m3；分布的均值．若随机变量X服从二项分布，当n100且p0.01时，二项分布近似于泊松分布，其中（2）求证：数列{}mn是等比数列，并用m表示数列的通项公式；enp−npi()=np，即XBnpPXiiN(,),()()==.现从该地区接种疫苗的人群中随机抽取1000人，（3）对任意的正整数k，PPF2k−22k−12k−1与FPP2k−+12k2k1的面积之比是否为定值？若是，请用m表示这个i!定值；若不是，请说明理由.按上述泊松分布近似计算：①求1000人中流感的患病率小于0.3%的概率约为多少；②设1000人中患流感的人数为X,求使得P()X=i最大时的X值.（参考数据：e−60.0025）数学试卷第3页（共3页）{#{QQABRYAowgg4kBaACI5LA0mkCEgQkJEiLWosRQCeqAwjgBFABAA=}#}