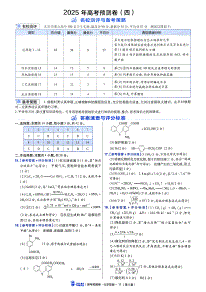
2024年高考考前逆袭卷（新高考新题型）02数学（考试时间：120分钟试卷满分：150分）全国新高考卷的题型会有所调整，考试题型为8（单选题）＋3（多选题）＋3（填空题）＋5（解答题），其中最后一道试题是新高考地区新增加的题型，主要涉及集合、数列，导数等模块，以解答题的方式进行考查。预测2024年新高考地区数列极有可能出现在概率与统计大题中，而结构不良型题型可能为集合或导数模块中的一个，出现在19题的可能性较大，难度中等偏上，例如本卷第19题。第I卷（选择题）一、选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的。1．已知一组数据，4，2，5，3的平均数为，且，是方程的两根，则这组数据的方差为（）A．10 B． C．2 D．2．，是两个向量集合，则等于（    ）A． B． C． D．3．在ΔABC中，内角A、B、C所对的边分别为a、b、c，若A、B、C成等差数列，3a、3b、3c成等比数列，则cosAcosB=（    ）A． B． C． D．4．在三棱锥中，底面为边长为3的正三角形，侧棱底面，若三棱锥的外接球的体积为，则该三棱锥的体积为（    ）A． B． C． D．5．有一排7只发光二极管，每只二极管点亮时可发出红光或绿光，若每次恰有3只二极管点亮，且相邻的两只不能同时点亮，根据三只点亮的不同位置，或不同颜色来表示不同的信息，则这排二极管能表示的信息种数共有种A．10 B．48 C．60 D．806．设，，，则(    )A． B． C． D．7．按照“碳达峰”､“碳中和”的实现路径，2030年为碳达峰时期，2060年实现碳中和，到2060年，纯电动汽车在整体汽车中的渗透率有望超过70%，新型动力电池迎来了蓬勃发展的风口.Peukert于1898年提出蓄电池的容量C（单位：），放电时间t（单位：）与放电电流I（单位：）之间关系的经验公式：，其中n为Peukert常数，为了测算某蓄电池的Peukert常数n，在电池容量不变的条件下，当放电电流时，放电时间；当放电电流时，放电时间.则该蓄电池的Peukert常数n大约为（    ）（参考数据：，）A． B． C． D．28．过双曲线的右焦点作渐近线的垂线，设垂足为（为第一象限的点），延长交抛物线于点，其中该双曲线与抛物线有一个共同的焦点，若，则双曲线的离心率的平方为A． B． C． D．二、选择题：本题共3小题，每小题6分，共18分．在每小题给出的选项中，有多项符合题目要求．全部选对的得6分，部分选对的得部分分，有选错的得0分．9．已知为虚数单位，以下四个说法中正确的是（    ）A．B．C．若，则复数对应的点位于第四象限D．已知复数满足，则在复平面内对应的点的轨迹为圆10．设直线系：，则下面四个命题正确的是（    ）A．点到中的所有直线的距离恒为定值B．存在定点不在中的任意一条直线上C．对于任意整数，存在正边形，其所有边均在中的直线上D．中的直线所能围成的正三角形面积都相等11．定义在上的偶函数满足，当时，.设函数，则下列结论正确的是（    ）A．的图象关于直线对称B．的图象在处的切线方程为C．D．的图象与的图象所有交点的横坐标之和为10第II卷（非选择题）三、填空题：本题共3小题，每小题5分，共15分．12．已知集合，集合，命题：，命题：，若是的充分条件，则实数的取值范围是.13．已知多项式，则.14．正方体中，是棱的中点，在侧面上运动，且满足平面.以下命题正确的有.①侧面上存在点，使得②直线与直线所成角可能为③平面与平面所成锐二面角的正切值为④设正方体棱长为1，则过点的平面截正方体所得的截面面积最大为四、解答题：本题共5小题，共77分．解答应写出文字说明、证明过程或演算步骤．15．（13分）已知的内角A，B，C的对边分别为a，b，c，且.(1)求a的值：(2)求证：；(3)的值16．（15分）如图1，在平面五边形中，，且，，，，将沿折起，使点到的位置，且，得到如图2所示的四棱锥．  (1)求证；平面；(2)若，求平面与平面所成锐二面角的余弦值．17．（15分）甲进行摸球跳格游戏．图上标有第1格，第2格，…，第25格，棋子开始在第1格．盒中有5个大小相同的小球，其中3个红球，2个白球（5个球除颜色外其他都相同）．每次甲在盒中随机摸出两球，记下颜色后放回盒中，若两球颜色相同，棋子向前跳1格；若两球颜色不同，棋子向前跳2格，直到棋子跳到第24格或第25格时，游戏结束．记棋子跳到第n格的概率为．(1)甲在一次摸球中摸出红球的个数记为X，求X的分布列和期望；(2)证明：数列为等比数列．18．（17分）焦点在轴上的椭圆的左顶点为，，，为椭圆上不同三点，且当时，直线和直线的斜率之积为．(1)求的值；(2)若的面积为1，求和的值；(3)在（2）的条件下，设的中点为，求的最大值．19．（17分）英国数学家泰勒发现了如下公式：其中为自然对数的底数，.以上公式称为泰勒公式.设，根据以上信息，并结合高中所学的数学知识，解决如下问题.(1)证明：；(2)设，证明：；(3)设，若是的极小值点，求实数的取值范围.